1)
Находим 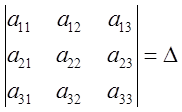 и
убеждаемся в том, что
и
убеждаемся в том, что ![]()
2)
Строим матрицу В, элементами
которой служат алгебраические дополнения соответствующих элементов определителя
матрицы А: 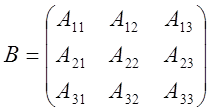
3)
Транспонируем В: 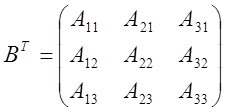
4)
Умножаем матрицу ![]() на коэффициент
на коэффициент ![]()
![]() :
:
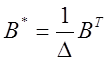 =
=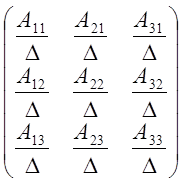
Покажем, что матрица В*-
искомая, т.е., ![]()
![]()
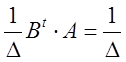
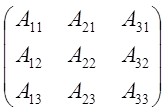
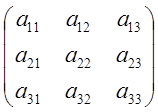 =
=
![]()
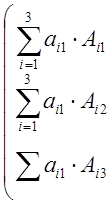
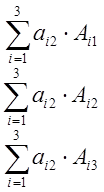
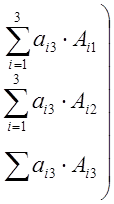 =
=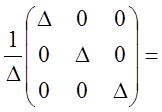
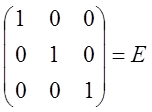 .
.
![]()
![]() Примем
Примем 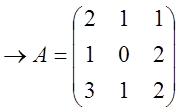 ;
; ![]()
Область применения:
1) число уравнений равно числу неизвестных
2)
член определителя матрицы ![]()
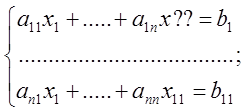
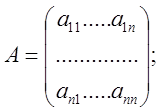
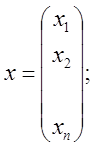
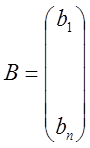
![]()
![]()
![]()
![]()
![]()
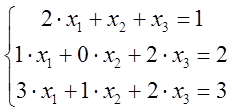
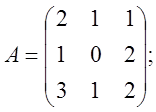
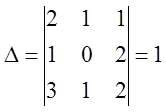 ;
; 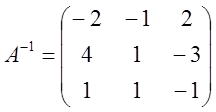
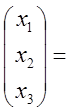
![]()
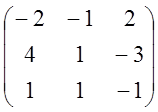
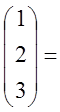
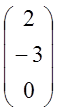
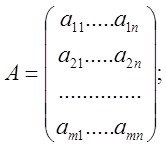
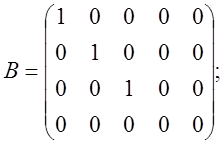
![]()
Минором ![]() го порядка матрицы
го порядка матрицы ![]() называют определитель квадратной матрицы,
получающейся из данной матрицы выделением производных
называют определитель квадратной матрицы,
получающейся из данной матрицы выделением производных![]() строк
и
строк
и ![]() столбцов.
столбцов.
Опр. Рангом матрицы![]() называют
наивысший порядок отличного от нуля минора матрицы
называют
наивысший порядок отличного от нуля минора матрицы ![]() и
обозначают
и
обозначают ![]()
Если ранг матрицы ![]() равен
равен ![]() , то это значит, что матрица имеет по
крайней мере один
, то это значит, что матрица имеет по
крайней мере один
нулевой минор ![]() -го
порядка, в то время как все миноры порядка
-го
порядка, в то время как все миноры порядка ![]() и выше
равны нулю.
и выше
равны нулю.
Элементарные операции над матрицами:
1) умножение строки (столбца) матрицы на любое отличное от нуля число;
2) сложение любой строки (столбца) матрицы с друой строкой (столбцом), предварительно умноженное на произвольное число;
3) Перестановка строк (столбцов) местами;
Определение Две матрицы, получающиеся одна из другой с помощью элементарных преобразований, называются эквивалентными.
Теорема. Эквивалентные матрицы имеют один и тот же ранг.
С помощью элементарных операций любая матрица приводится к эквивалентной матрице канонической структуры. (Главная диагональ или ее часть -единицы, а остальные элементы - нули).
Пример. 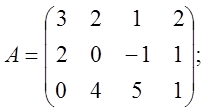
![]() ~
~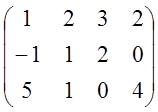 ~
~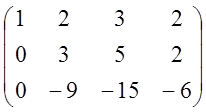 ~
~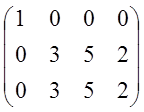 ~
~
~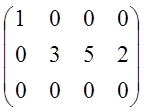 ~
~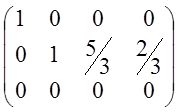 ~
~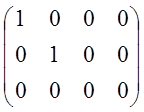 ;
; 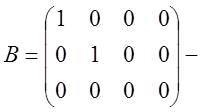 каноническая структура.
каноническая структура.
![]()
Понятие об линейной зависимости. 
![]()
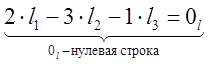
Определение Говорят, что строки ![]() линейно
зависимы, если их линейная комбинация
линейно
зависимы, если их линейная комбинация 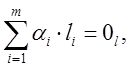 где
где ![]() ,
, ![]() числа не
равные нулю одновременно.
числа не
равные нулю одновременно.
Если же равенство 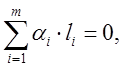 выполняется
только при всех нулевых
выполняется
только при всех нулевых ![]() то строки
то строки ![]() называют линейно независимыми.
называют линейно независимыми.
![]()
![]()
![]()
![]() -линейно
независимые
-линейно
независимые
Теорема. Если ранг матрицы равен![]() , то в
этой матрице можно найти
, то в
этой матрице можно найти![]() линейно- независимых
строк (столбцов), через которые линейно выражаются все линейные строки.
линейно- независимых
строк (столбцов), через которые линейно выражаются все линейные строки.
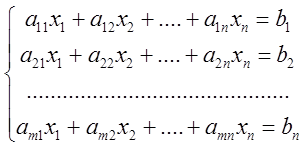
Очевидно, что ![]() , т.к. каждый минор матрицы
, т.к. каждый минор матрицы ![]() будет и минором матрицы
будет и минором матрицы ![]() но не наоборот.
но не наоборот.
(1)
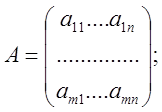
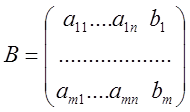
Опр: Матрица ![]() , получится из матрицы
, получится из матрицы ![]() путем добавления столбца свободных членов,
называется расширенной матрицей системы.
путем добавления столбца свободных членов,
называется расширенной матрицей системы.
Опр. Две совместные системы (1) называют равносильными, если они имеют одно
и то же множество решений.
Элементарные операции:
1) перемена местами любых уравнений;
2) умножение любого из уравнений на число, отличное от нуля.
3) прибавление к одному из уравнений другого, предварительно умноженного на любое число.
Теорема. Элементарные преобразования переводит систему в новую систему, равносильную исходной.
Примечание. 1. Если в результате элементарных
преобразований в системе появилось уравнение вида ![]() , то
оно может быть отброшено.
, то
оно может быть отброшено.
2.Если в результате эл. операций в системе появилось
уравнение вида![]() ,
,![]() то такое
уравнение, а значит и вся система будут несовместимыми.
то такое
уравнение, а значит и вся система будут несовместимыми.
Теорема
Краменора-Капелли. Для того, чтобы система (1) была совместной, необходимо и
достаточно, чтобы ранг матрицы ![]() совпадал с рангом ее
расширенной матрицы:
совпадал с рангом ее
расширенной матрицы:![]()
![]() Причем, если при выполнении условия 2)
окажется, что ранг матрицы
Причем, если при выполнении условия 2)
окажется, что ранг матрицы ![]() равен числу неизвестных
равен числу неизвестных
![]() , то система (1) будет иметь единственное
решение, если же ранг будет меньше числа неизвестных, то система будет
неопределенной.
, то система (1) будет иметь единственное
решение, если же ранг будет меньше числа неизвестных, то система будет
неопределенной.
Алгоритм.
Пр. Не решая системы уравнений, выяснить вопрос существования и единственности
и решения.
1).
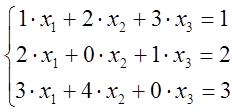
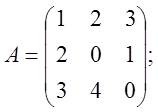
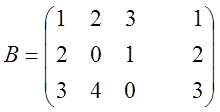 ~ ~
~ ~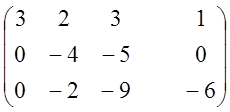 ~
~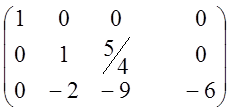 ~
~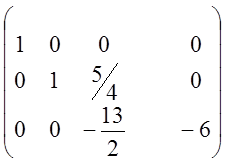 ~
~
~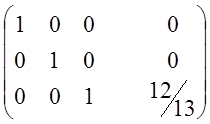 ~
~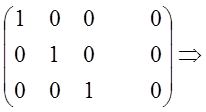
![]()
![]() система
определенная, т.к.
система
определенная, т.к. ![]()
2).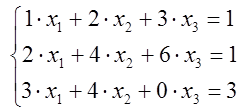
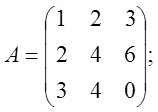
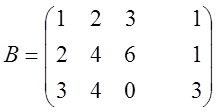 ~
~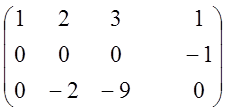 ~
~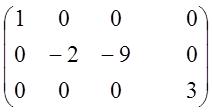 ~
~
~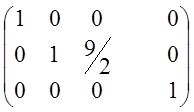 ~
~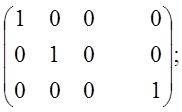
![]()
![]()
![]()
![]() система несовместная.
система несовместная.
3).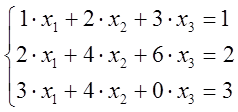
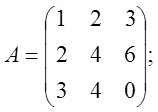
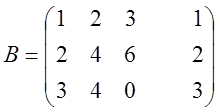 ~
~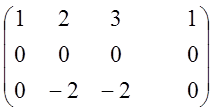 ~
~
~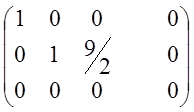 ~
~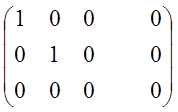
![]() система неопределенная.
система неопределенная.
Доказательство теории Кронекера-Копелли.
1). Необходимость; Пусть система (1)-совместная ![]() -одно из ее решений
-одно из ее решений
(существует)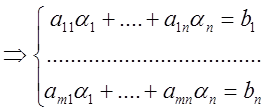
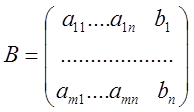 ~
~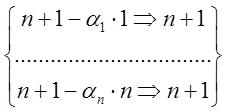 ~
~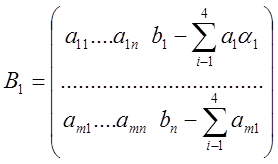 =
=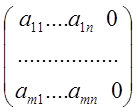 ;
;![]()
![]()
2) Достаточность; Пусть ![]() .
Покажем что система совместная.
.
Покажем что система совместная.
![]()
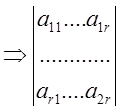
![]()
Если отличный от нуля определитель не занимает левый верхний угол, то путем перенумерации переменных и уравнений всегда это можно сделать.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.