2) 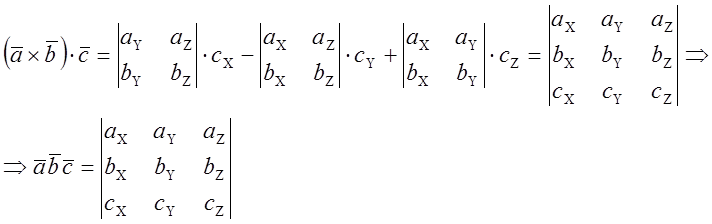
Свойства: ![]()
Геометрический смысл. ![]() - Площадь основания.
- Площадь основания.
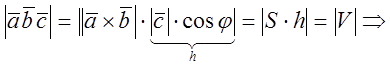 смешанное произведение
смешанное произведение ![]() с точностью до знака равно объему
параллелепипеда построенного на векторах
с точностью до знака равно объему
параллелепипеда построенного на векторах ![]() как на
сторонах.
как на
сторонах.![]()
Определение Три вектора лежащие в одной плоскости, называются коллинеарными.
Теорема. Для того, чтобы три
вектора ![]() были коллинеарными, необходимо и
достаточно, чтобы их смешанное произведение равнялось нулю.
были коллинеарными, необходимо и
достаточно, чтобы их смешанное произведение равнялось нулю.
![]()
Доказательство. 1) Пусть ![]()
2)Пусть![]() Если допустить
противное, т.е. что
Если допустить
противное, т.е. что ![]() - не коллинеарные, то существует
параллелепипед с
- не коллинеарные, то существует
параллелепипед с ![]() что противоречит условию. Примечание.
Объем пирамиды, построенной на ребрах
что противоречит условию. Примечание.
Объем пирамиды, построенной на ребрах ![]() равен
равен ![]() от объема параллелепипеда, построенного
на тех же ребрах.
от объема параллелепипеда, построенного
на тех же ребрах.
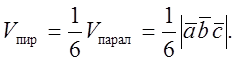
Условие компланарности трех
векторов: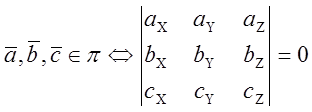 .
.
Определение Уравнением линии
1 на плоскости ![]() называется уравнение двух
переменных
называется уравнение двух
переменных ![]() , которому удовлетворяют координаты любой
т.
, которому удовлетворяют координаты любой
т.![]() и не удовлетворяют координаты любой т.
и не удовлетворяют координаты любой т.![]()
Дано: ![]()
Найти уравнение прямой![]()
Определение Вектор N (А,B) перпендикулярный к прямой l, называется нормальным вектором этой прямой.
Решение. ![]() текущая точка прямой l
текущая точка прямой l
![]()
Имеем: (1)![]() Уравнение прямой проходящей через заданную
Уравнение прямой проходящей через заданную
точку![]() перпендикулярную
заданному вектору
перпендикулярную
заданному вектору ![]() . Вывод: Любая
прямая на плоскости описывается уравнением 1-ой степени относительно
неизвестных
. Вывод: Любая
прямая на плоскости описывается уравнением 1-ой степени относительно
неизвестных ![]() , в котором
, в котором ![]()
![]() , где
, где ![]() (2)
(2)
Обратно: пусть ![]() -уравнение 1-й степени, причем
-уравнение 1-й степени, причем ![]() .
Пусть для определенности
.
Пусть для определенности ![]() . Тогда
. Тогда 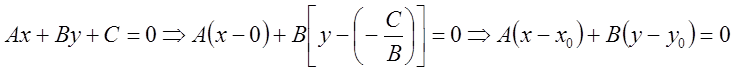 при
при 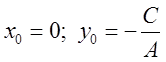 .
.
Вывод: Любое уравнение первой степени есть уравнение
некоторой прямой, лежащей на плоскости ![]() :
:
![]()
![]() - прямая.
- прямая.
![]() - общее уравнение прямой.
- общее уравнение прямой.
Частные случаи:
А) ![]() ;
;
Б) 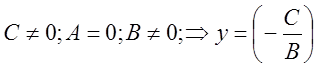 ;
; ![]() ;
;
В) 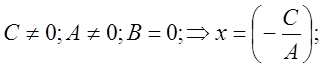
![]() .
.
Определение:
Вектор ![]() , коллинеарный заданной прямой
, коллинеарный заданной прямой ![]() , называется ее направляющим вектором.
, называется ее направляющим вектором.
Дано:
![]() - направляющий вектор
- направляющий вектор ![]() ;
; ![]() .
.
Найти
уравнение прямой ![]() .
.
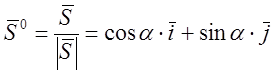
Решение.
![]() .
. ![]()
![]()
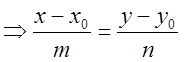 - каноническое уравнение прямой, проходящей
через точку
- каноническое уравнение прямой, проходящей
через точку ![]() параллельно вектору
параллельно вектору ![]() .
.
Пусть
направляющим вектором служит единичный вектор ![]()
![]()
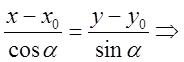
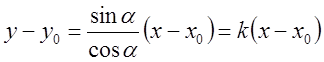 ,
где
,
где ![]() . Имеем:
. Имеем: ![]() -
уравнение прямой, проходящей через заданную точку
-
уравнение прямой, проходящей через заданную точку ![]() с
заданным угловым коэффициентом
с
заданным угловым коэффициентом ![]()
![]() .
.
Дано:
![]() ;
; ![]() .
Составить уравнение прямой
.
Составить уравнение прямой ![]() .
.
Решение.
![]()
![]()
![]()
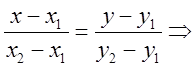
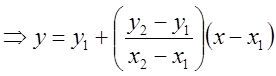 - уравнение прямой, проходящей через две
заданные точки с угловым коэффициентом
- уравнение прямой, проходящей через две
заданные точки с угловым коэффициентом 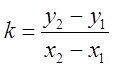 .
.
Уравнение
прямой в образах: ![]()
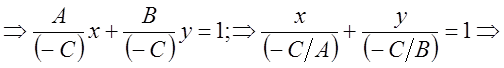
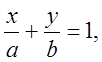 где
где ![]() .
.
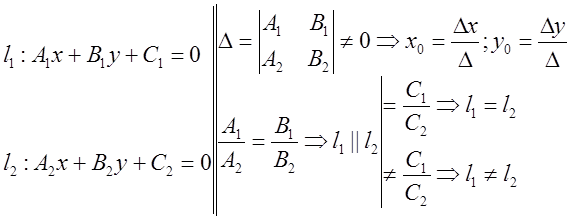
Примечание.
Если ![]() , т.е. прямые
, т.е. прямые ![]() и
и ![]() , заданные уравнениями общего вида,
пересекаются, то уравнение
, заданные уравнениями общего вида,
пересекаются, то уравнение ![]() описывает пучок
прямых, проходящих через точку пересечения
описывает пучок
прямых, проходящих через точку пересечения ![]() .
.
![]()
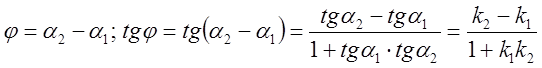 .
.
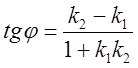
Примечание.
1)
Если ![]() , то
, то ![]() . {Необходимым и достаточным
условием параллельности двух прямых является равенство их угловых коэффициентов}.
. {Необходимым и достаточным
условием параллельности двух прямых является равенство их угловых коэффициентов}.
2)
Если ![]() н/с
н/с 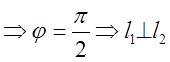 .
.
Вывод:
Для того, чтобы прямые ![]() и
и ![]() были
перпендикулярны, необходимо и достаточно, чтобы
были
перпендикулярны, необходимо и достаточно, чтобы ![]() .
.
Дано:
![]()
Найти:
![]()
Решение.
1.
![]() ;
;
2.
![]() ;
;
3.
![]() , где
, где ![]() ;
;
4.
![]()
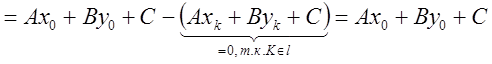 ;
;
5.
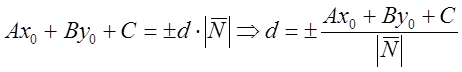 .
.
Вывод: 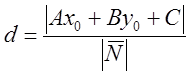 .
.
Определение: Кривой
второго порядка называется линия, определяемая уравнением второй степени
относительно переменных ![]() и
и ![]() :
:
![]() (1)
(1)
1.
Окружность – геометрическое место
точек, равноудаленных от одной точки ![]() , именуемой центром.
, именуемой центром.
![]()
![]()
![]() - (2)
- (2)
уравнение
окружности радиуса ![]() с центром в точке
с центром в точке ![]() .
.
(1),(2)![]()
![]() - частный случай
уравнения (1).
- частный случай
уравнения (1).
Обратная
задача. Что определяет уравнение (1), если ![]() , т.е.
, т.е. ![]()
![]() , где
, где ![]()
А)
![]() , где
, где ![]() -
уравнение (2) окружности.
-
уравнение (2) окружности.
Б)
![]() окружность выраждается в точку
окружность выраждается в точку ![]() .
.
В)
![]() не существует геометрического образа.
не существует геометрического образа.
Определение. Эллипсом
называется геометрическое место точек, сумма расстояний каждой из которых до
двух фиксированных точек ![]() и
и ![]() , именуемых фокусами, есть число
постоянное, равное
, именуемых фокусами, есть число
постоянное, равное ![]() , причем
, причем ![]() ,
где
,
где ![]() - расстояние между фокусами.
- расстояние между фокусами.
Выбор системы координат:
1) Ось ОХ проходит через фокусы.
2) Фокусы располагаются симметрично относительно начала координат.
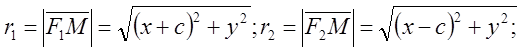
![]() фокальные радиусы;
фокальные радиусы; ![]()
![]()
![]()
![]()
![]() ;
;
![]()
![]()
![]() .
.
Имеем
![]() (3).
(3).
![]()
![]() (4)
(4) ![]()
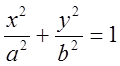 (5).
(5).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.