![]()
![]()
![]() , где
, где![]()
![]() .
.
Теорема 9. Предел произведения двух функций равен произведению пределов этих функций, при условии, что последние существуют.
![]() .
.
Доказательство. ![]() ;
;![]()
![]() , где
, где ![]() .
.![]() .
.
Следствие 1. Постоянный множитель выносится за знак предела:
![]()
Следствие 2. Предел степени равен степени предела:
![]() .
.
Теорема
10. Предел частного от деления двух функций ![]() и
и![]() равен частному пределов
этих функций, при условии, что эти пределы существуют и предел знаменателя не
равен нулю.
равен частному пределов
этих функций, при условии, что эти пределы существуют и предел знаменателя не
равен нулю.
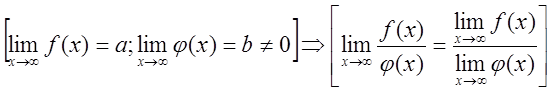 .
.
Доказательство. ![]() ;
;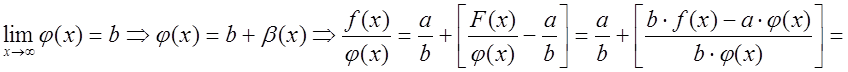
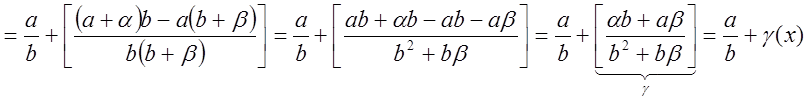 , где
, где ![]()
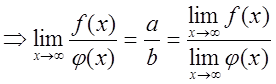 , что и требовалось доказать.
, что и требовалось доказать.
Теорема
11. При ![]() предел отношения двух многочленов равен
отношению коэффициентов при высших степенях
предел отношения двух многочленов равен
отношению коэффициентов при высших степенях ![]() этих
многочленов, если степени
этих
многочленов, если степени ![]() многочлена числителя
равна
многочлена числителя
равна ![]() степени многочлена знаменателя. Если
степени многочлена знаменателя. Если ![]() , то предел равен нулю. Если
, то предел равен нулю. Если ![]() , то предел равен бесконечности.
, то предел равен бесконечности.
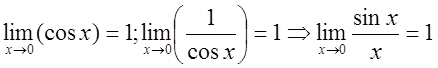 .
. 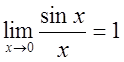
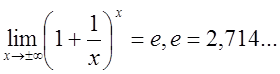 Пусть
Пусть
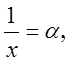 тогда
тогда 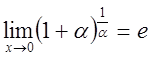
1)
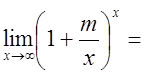
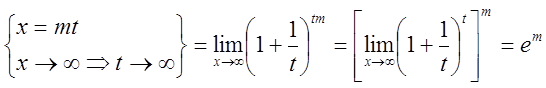 .Итак
.Итак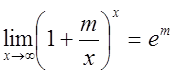 .
.
2)
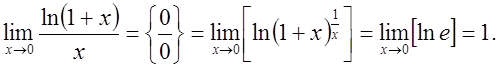 Итак
Итак 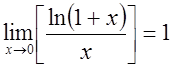 ;
;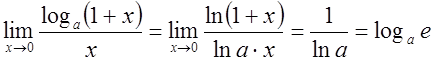
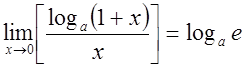
3)
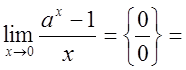
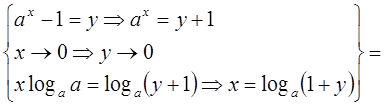
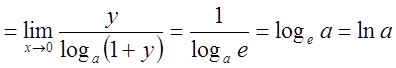
Итак 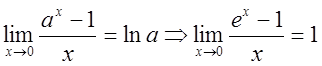 .
.
4)
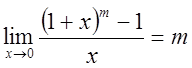 .
.
Примеры вычисления пределов.
1)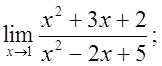 2)
2)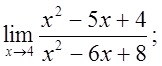 3)
3)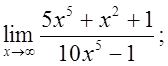 4)
4)
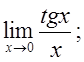 5)
5)
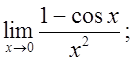 6)
6)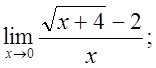 7)
7)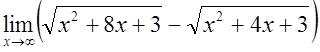 ; 8)
; 8)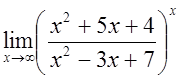 .
.
![]() при
при ![]() (или
(или ![]() ).
).
Определение. Если
существует отличный от нуля и бесконечный предел отношения двух ![]() , то такие
, то такие ![]() называют
называют
![]() одного и того же порядка малости.
одного и того же порядка малости.
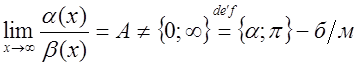 одного
порядка.
одного
порядка.
Если 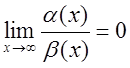 , то
, то ![]() есть
есть ![]() более высокого порядка малости, чем
более высокого порядка малости, чем ![]() .
.
Определение. Если
предел отношения двух ![]() равен
равен ![]() ,
то такие
,
то такие ![]() называют эквивалентными.
называют эквивалентными.
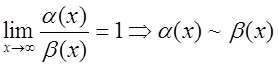 .
.
Таблица эквивалентности: (Пусть ![]() ) :
) :
![]() ;
;![]() ;
;![]() ; tg
; tg![]() ;
; ![]() ;
; ![]() ; arctg
; arctg![]() .
.
Теорема
. Предел
отношения двух ![]() функций равен пределу отношения
эквивалентных им функций (если последний предел существует).
функций равен пределу отношения
эквивалентных им функций (если последний предел существует).
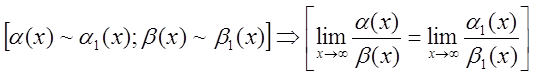
Доказательство.
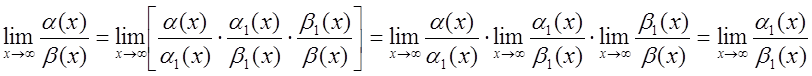 , т.к.
, т.к.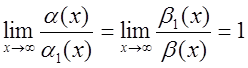 .
.
Примеры.
1) 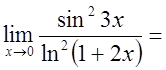
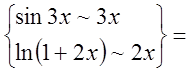
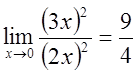 .
.
2)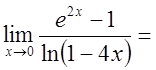
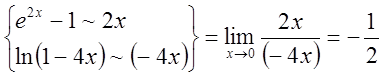 .
.
3)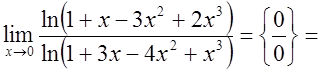
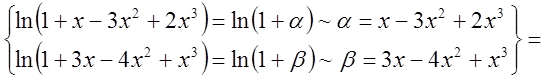
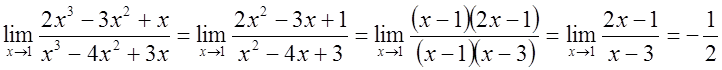 .
.
Определение. Функция ![]() называется непрерывной в точке
называется непрерывной в точке ![]() , если
, если
1)функция определена как в самой точке ![]() , так и в некоторой её окрестности;
, так и в некоторой её окрестности;
2)существует конечные левосторонний и правосторонний пределы:
![]() ;
; ![]() .
.
3)левосторонний
и правосторонний пределы совпадают со значением функции в точке ![]() , т.е.
, т.е.
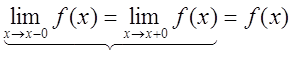 (1).
(1).
![]()
![]() .
.
Если учесть, что ![]() , то
, то 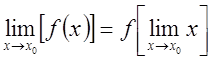 .
.
Определение. Точка ![]() , в которой функция
, в которой функция ![]() -
непрерывна, называется точкой непрерывности данной функции.
-
непрерывна, называется точкой непрерывности данной функции.
Точка ![]() называется точкой
разрыва функции
называется точкой
разрыва функции![]() , если она принадлежит области
определения функции или её границе и не является точкой непрерывности.
, если она принадлежит области
определения функции или её границе и не является точкой непрерывности.
Различают точки разрыва 1 и 2 рода.
Определение. Если в точке разрыва ![]() существует
конечные левосторонний и правосторонний пределы, то эта точка называется точкой
разрыва 1-го рода. Точка разрыва, не являющаяся точкой разрыва 1-го рода,
называется точкой разрыва 2-го рода.
существует
конечные левосторонний и правосторонний пределы, то эта точка называется точкой
разрыва 1-го рода. Точка разрыва, не являющаяся точкой разрыва 1-го рода,
называется точкой разрыва 2-го рода.
Теорема 1. Для
того, чтобы функция ![]() и была непрерывной в точке
и была непрерывной в точке ![]() , необходимо и достаточно, чтобы бесконечно
малому приращению аргумента соответствовало бесконечно малое приращение
функции, т.е.
, необходимо и достаточно, чтобы бесконечно
малому приращению аргумента соответствовало бесконечно малое приращение
функции, т.е.![]() .
.
Доказательство.
![]()
![]() .
.
Теорема 2.
Если функции ![]() и
и ![]() непрерывны
в точке
непрерывны
в точке ![]() , то их сумма и произведение также
непрерывны в точке
, то их сумма и произведение также
непрерывны в точке ![]() .Если, кроме того
.Если, кроме того ![]() , то функция
, то функция ![]() - также
непрерывна в точке
- также
непрерывна в точке ![]() .
.
Теорема 3.
Сложная функция ![]() ,
образованная из двух непрерывных функций
,
образованная из двух непрерывных функций ![]() и
и ![]() , есть непрерывная функция.
, есть непрерывная функция.
Теорема 4. Если функция ![]() непрерывна
на замкнутом отрезке
непрерывна
на замкнутом отрезке ![]() , то:
, то:
1) эта функция ограничена на этом отрезке;
2) эта функция на этом отрезке достигает своего наибольшего и наименьшего значений;
3) если на концах отрезка функция принимает значения разных знаков, то внутри этого отрезка существует по крайней мере одна точка, в которой функция равна нулю.
![]() ;
;![]() ;
;![]() .
.
![]() закон движения
точки.
закон движения
точки. 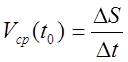 ;
;![]()
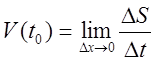 -мгновенная скорость
точки в момент времени.
-мгновенная скорость
точки в момент времени.
Определение. Предельное положение секущей ![]() при
условии, что точка
при
условии, что точка ![]() , двигаясь вдоль кривой
, двигаясь вдоль кривой ![]() , бесконечно близко приближается к точке
, бесконечно близко приближается к точке ![]() , называется касательной.
, называется касательной.
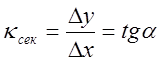 ;
;![]()
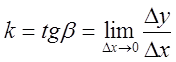 - тангенс угла наклона касательной (угловой коэффициент)
в точке
- тангенс угла наклона касательной (угловой коэффициент)
в точке ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.