![]() .
. ![]() . Задаем разложение нового базиса по
старому
. Задаем разложение нового базиса по
старому 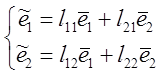 (1)
(1)
![]() -старый базис
-старый базис
![]() -новый базис.
-новый базис.
То есть 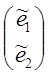 =Lт
=Lт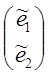 ,где Lт
,где Lт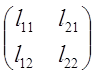 .
.
![]() =
=![]() =
=![]() +
+![]() =
=![]() +
+![]() =>
=>
=>
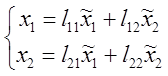 (2)
(2) 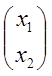 =L
=L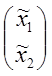 , где L=
, где L=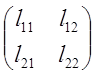 .
.
Вывод: Если новый базис задан формулами (1), то старые
координаты любого вектора ![]() выражаются чурез его
новые координаты по формулам (2).
выражаются чурез его
новые координаты по формулам (2).
х=L![]() =>
=>![]() L-1 х где х=
L-1 х где х=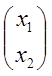 ,
, ![]() =
=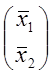 .
.
Частный случай ![]() =
=![]() ;
; ![]() =
=![]() , где
, где ![]() ,
,![]() ортопорогальные базисы.
ортопорогальные базисы.
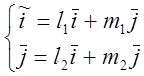 Lт
Lт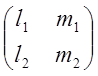 . L
. L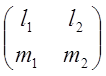 .
.
![]() =>
=> ![]() ;
;
![]() =>
=> ![]() ;
;
![]() => l1l2+m1m2=0.
=> l1l2+m1m2=0.
LтL=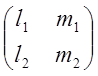
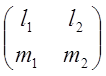 =
= =
=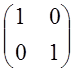 =Е
=Е
LтL=Е => LтL-1.
Определение: Матрица L, удовлетворяющая условию LтL-1, называется ортогональной.
Вывод: При переходе от ортонормального
базиса ![]() к
ортонормальному базису
к
ортонормальному базису ![]() получается формулы
преобразования координатой (2), матрица которых является ортогональной. То есть
х=L
получается формулы
преобразования координатой (2), матрица которых является ортогональной. То есть
х=L![]() =>
=> ![]() =L-1х= Lтх (3).
=L-1х= Lтх (3).
1) Пусть дано линейное преобразование:
![]() ,
, ![]() =
=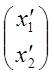 ; х=
; х=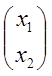 , А=
, А=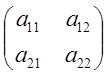 ;
;  (4)
(4)
2)
Пусть задан переход от старого
базиса ![]() к новому базису
к новому базису ![]() .
.
х=L![]() где L=
где L=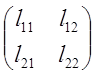 ;
; ![]() =
= .
.
![]() -старые координаты
вектора
-старые координаты
вектора ![]()
![]() -новые координаты
вектора
-новые координаты
вектора ![]()
![]() -старые координаты
вектора
-старые координаты
вектора ![]() =А
=А![]()
![]() -старые координаты
вектора
-старые координаты
вектора ![]() .
.
Имеет: х=L![]() ;
; ![]() =L
=L![]() ;
; ![]() =А
=А![]() => L
=> L![]() =АL
=АL![]() (умножим на L-1) L-1L
(умножим на L-1) L-1L![]() =
=
=L-1АL![]() =>
=> ![]() =(L-1АL)
=(L-1АL)![]() - координатное представление данного
линейного преобразования
- координатное представление данного
линейного преобразования ![]() =
=![]()
![]() в новом базисе.
в новом базисе.
То есть ![]() =
=![]()
![]() , где
, где ![]() =L-1АL.
=L-1АL.
Пример: Дано координатное представление некоторого линейного преобразования в базисе. ![]() :
: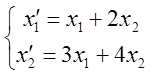
Найти координатное представление того же
преобразования в базисе ![]() , если
, если 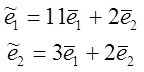 .
.
Решение имеет: А=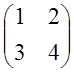 ; Lт=
; Lт= => L=
=> L=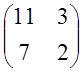
Доказательство
L=1![]() 0 =>
L-1=
0 =>
L-1=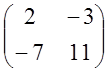 ; =>
; => ![]() =L-1AL=
=L-1AL=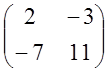
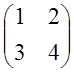
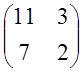 =
=
=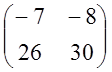
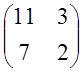 =
= .
.
Ответ: 
Определение:
Пусть дано линейное преобразование: ![]() =А
=А![]() .
.
Вектор ![]() (не равный нулю)
называется собственным числом вектора
(не равный нулю)
называется собственным числом вектора ![]()
Теорема:
Если ![]() -собственный вектор данного
преобразования, то всякий не равный нулю коллинеарный ему вектор
-собственный вектор данного
преобразования, то всякий не равный нулю коллинеарный ему вектор ![]() =
=![]()
![]() будет также собственным вектором данного
преобразования с тем же собственным числом.
будет также собственным вектором данного
преобразования с тем же собственным числом.
Доказательство: ![]() -собственный
вектор => А
-собственный
вектор => А![]() =
=![]()
![]() . Пусть
. Пусть ![]() =
=![]()
![]() . Тогда А
. Тогда А![]() =А(
=А(![]()
![]() )=А
)=А![]() (
(![]() )=
)=![]()
![]()
![]() =(
=(![]()
![]() )
)![]() =
=![]() (
(![]()
![]() )=
)=![]()
![]()
А![]() =
=![]()
![]()
Пусть ![]() =А
=А![]() - на плоскости, имеющее два собственных
вектора
- на плоскости, имеющее два собственных
вектора ![]() с собственными числами
с собственными числами ![]() и
и ![]() .
.
Так как ![]() и
и ![]() -не коллинеарные, то примем их в качестве
базиса. Найдем координатное представление л/пр в это базисе:
-не коллинеарные, то примем их в качестве
базиса. Найдем координатное представление л/пр в это базисе: 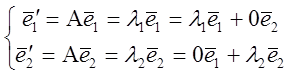 =>
=>
=>
Ат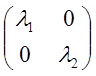 =А => А
=А => А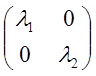 .
.
Вывод: Если в качестве базиса приняты собственные
векторы ![]() данного линейного преобразования, то
матрица А этого преобразования получает диагональный вид, причем по диагонали
располагаются собственные числа векторов
данного линейного преобразования, то
матрица А этого преобразования получает диагональный вид, причем по диагонали
располагаются собственные числа векторов ![]() .
.
В этом базисе л/прие представляется формулами: 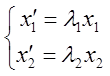
Найдем все собственные векторы л/прие А, имеющего в
некотором базисе ![]() координатное представление
координатное представление 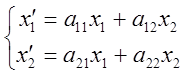 с матрицей А=
с матрицей А=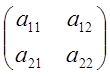
Пусть ![]() =(l;m)-искомый
собственный вектор.
=(l;m)-искомый
собственный вектор.
Тогда: ![]() =>
=> 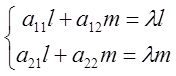
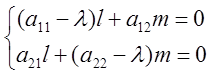
Для получения нулевых решений необходимо, чтобы 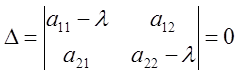
Уравнение 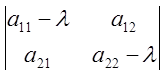 =0 (2) называется
характеристическим.
=0 (2) называется
характеристическим.
Вывод: Чтобы найти все собственные векторы линейного
преобразования, нужно решить характеристическое уравнение (2); соответствующие
числу ![]() собственные векторы находятся из системы
(1).
собственные векторы находятся из системы
(1).
Пример: Найти собственные векторы линейного преобразования:
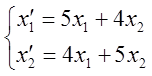 А=
А=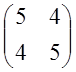 Решение 1.
Составляем уравнение
Решение 1.
Составляем уравнение  =0
=> (5-
=0
=> (5-![]() )2-16=0 => (5-
)2-16=0 => (5-![]() -4)(5-
-4)(5-![]() +4)=0 => (1-
+4)=0 => (1-![]() )(9-
)(9-![]() )=0
)=0 ![]() =1;
=1; ![]() =9
=9
а) ![]() =1;
=1; ![]() =
=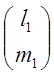 ;
; 
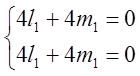
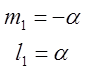 =>
=>
=> ![]() =
=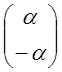 =
=![]()
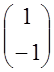 ,
, ![]() R\
R\![]() .
. 
б) ![]() =9;
=9; ![]() =
=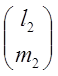 ;
; 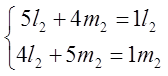
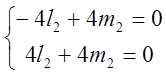
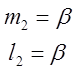 =>
=>
ð
![]() =
=![]() =
=![]()
![]() ,
, ![]() R\
R\![]() .
.  .
.
Определение: Квадратичной формы от двух переменных ![]() и
и ![]() называется
однородный многочлен второй степени относительно этих переменных:
называется
однородный многочлен второй степени относительно этих переменных:
F![]() =
=![]() .
. ![]()
Пусть в базисе ортогональном, ![]() вектор
вектор
![]() имеет координаты
имеет координаты 
F![]() =
=![]() =
=![]() .
.
Рассмотрим линейное преобразование ![]() , которое в базисе
, которое в базисе ![]() ,
имеет координатный вид
,
имеет координатный вид 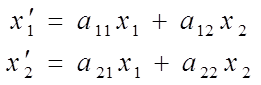
Тогда F![]() =
=![]() =(
=(![]() т)
т)![]() =
= ![]() А
А![]()
То есть F![]() =
=![]() тА
тА![]()
Придем к новому ортогональному базису ![]() :
:
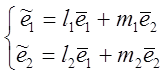
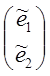 =Lт
=Lт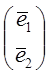 , где Lт
, где Lт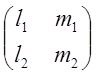
В новом базисе ![]() матрице
преобразования будет иметь вид
матрице
преобразования будет иметь вид ![]() L-1AL, а так как мы имеем дело с
ортогональными базисами то L-1=Lт =>
L-1AL, а так как мы имеем дело с
ортогональными базисами то L-1=Lт => ![]() LтAL.
LтAL.
Определение: Квадратная
форма имеет каконический вид, если ![]() . В этом случае
матрица формы является диагональной : А=
. В этом случае
матрица формы является диагональной : А=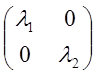 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.