Определение. Любая прямая, параллельная заданной прямой l и проходящая через заданную прямую L называется образующей.
Опр. Множество всех образующих составляет цилиндрическую поверхность, соответствующую кривой L.
Пример.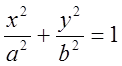 - уравнение эллиптического
цилиндра в пространстве.
- уравнение эллиптического
цилиндра в пространстве.
![]() -уравнение
параболического цилиндра в пространстве.
-уравнение
параболического цилиндра в пространстве.
Определение. Поверхность состоящая из прямых, проходящих через заданную вершину p и пересекающая заданную направляющую L, называется канонической поверхностью.
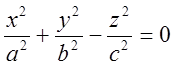 -уравнение эллиптического конуса.
-уравнение эллиптического конуса.
1. Эллипсоиды. 2.Гиперболоиды.
а) Однополостный б) Двухполостный
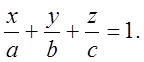
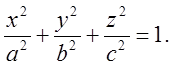 |
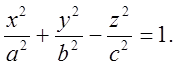
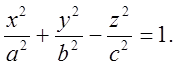
3.Параболоиды. а) Эллиптический б) Гиперболический
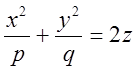
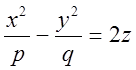
Определение. Если
каждому элементу ![]() по определённому правилу
поставлен в соответствие элемент
по определённому правилу
поставлен в соответствие элемент ![]() , то говорят, что задана
функция
, то говорят, что задана
функция ![]() , отображающая
, отображающая ![]() на
на ![]() :
: ![]() .
.
То множество ![]() значений аргумента
значений аргумента ![]() ,
при котором выражение, задающее функцию, имеет смысл, называют областью
её определения. Множество значений
,
при котором выражение, задающее функцию, имеет смысл, называют областью
её определения. Множество значений ![]() -
область значений.
-
область значений.
Определение. Число ![]() называется пределом функции
называется пределом функции ![]() при
при ![]() и
обозначается
и
обозначается ![]() если для любого сколь угодно
малого
если для любого сколь угодно
малого ![]() существует такое число
существует такое число ![]() , в общем случае зависящее от выбора
, в общем случае зависящее от выбора ![]() , что для всех
, что для всех ![]() будет
выполняться неравенство
будет
выполняться неравенство ![]() , то есть
, то есть
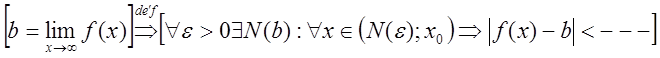 (2)
(2)
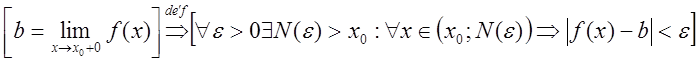 (3)
(3)
В дальнейшем все
определения и доказательства будут даваться для случая ![]() ,
для всех же остальных случаев всё аналогично.
,
для всех же остальных случаев всё аналогично.
Пример. Доказать что 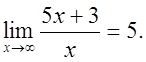
Решение. 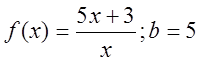 .
.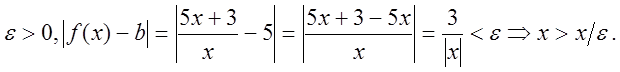
Итак: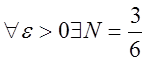
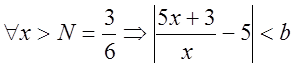 ,что
означает, что
,что
означает, что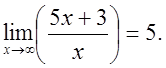
Определение. Функция ![]() называется бесконечно малой функцией при
называется бесконечно малой функцией при ![]() , если её предел при
, если её предел при ![]() равен нулю:
равен нулю:
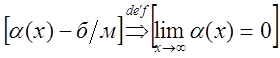 (3)
(3)
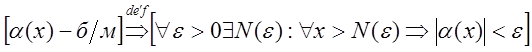 (4)
(4)
Определение. Функция ![]() называется ограниченной на бесконечности,
если существует такое положительное число
называется ограниченной на бесконечности,
если существует такое положительное число ![]() , что
для всех
, что
для всех ![]() выполняется равенство
выполняется равенство ![]() , т.е.
, т.е.
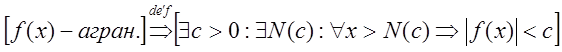 (5)
(5)
Теорема 1 Если функция имеет предел при ![]() ,то она ограничена на некотором бесконечном
интервале
,то она ограничена на некотором бесконечном
интервале ![]()
Теорема
2 Если функция ![]() имеет
предел при
имеет
предел при ![]() , отличный от нуля, то функция
, отличный от нуля, то функция ![]() ограничена при
ограничена при ![]() .
.
Следствие. Бесконечно-малая функция (при![]() ) ограничена (при
) ограничена (при![]() ).
).
Теорема
3 Если
![]() и
и![]() являются
являются ![]() функциями при
функциями при ![]() , то и
их сумма
, то и
их сумма ![]() также являются
также являются ![]() функцией
при
функцией
при ![]() .
.
Доказательство. ![]()
![]()
Выбираем ![]() .Тогда
.Тогда![]() и
и ![]() одновременно.
одновременно.
Имеем:![]() -
-![]() функция.
функция.
Следствие. Конечная сумма бесконечно- малых функций есть функция бесконечно малая.
Теорема
4. Произведение бесконечно- малой функции ![]() есть функция бесконечно- малая ,
т.е.
есть функция бесконечно- малая ,
т.е. ![]() .
.
Следствие. Так как любая ![]() .функция
есть функцией ограниченной, то произведение двух
.функция
есть функцией ограниченной, то произведение двух ![]() .
функций есть функция
.
функций есть функция![]() .
.
Следствие. Произведение ![]() функции
на число есть функция
функции
на число есть функция ![]() .
.
Следствие. Произведение конечного числа ![]() функций
есть функция
функций
есть функция ![]() .
.
Теорема
5. Частное от деления функции ![]() ,бесконечно-малой при
,бесконечно-малой при ![]() , на функцию
, на функцию ![]() , предел
которой отличен от нуля при
, предел
которой отличен от нуля при ![]() , является функцией
, является функцией ![]() .
.
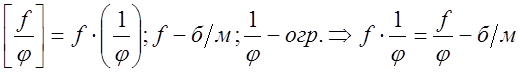 .
.
Теорема
6. Если функция ![]() имеет
предел (при
имеет
предел (при![]() ), равный
), равный ![]() , то она
может быть представлена в виде суммы этого предела и некоторой
, то она
может быть представлена в виде суммы этого предела и некоторой ![]() функции
функции ![]() , то
предел этой функции равен
, то
предел этой функции равен ![]() , т.е.
, т.е.
![]() (6).
(6).
Доказательство. 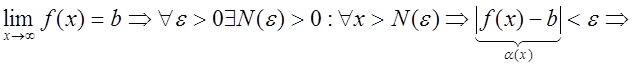
![]()
![]() где
где![]() .
.
Теорема
7.(обратная) Если некоторая функция ![]() может быть представлена в виде суммы
некоторого числа
может быть представлена в виде суммы
некоторого числа ![]() и
и ![]() функции
функции ![]() , то предел этой функции равен
, то предел этой функции равен ![]() , т.е.
, т.е.
![]()
Доказательство. ![]()
![]() . Что
и требовалось доказать.
. Что
и требовалось доказать.
Теорема 8. Предел суммы двух функций равен сумме пределов этих функций, если последние существуют.
![]() .
.
Доказательство.![]() ;
; ![]() .
.
![]()
![]()
![]() где
где ![]() .
.
![]() .
.
Теорема 9. Предел произведения двух функций равен произведенияю пределов этих реакций, при условии, что последние существуют.
![]()
Доказательство. ![]() ;
; ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.