2. Если производная функции ![]() на
интервале
на
интервале ![]() существует и отрицательна, то на этом
интервале функция
существует и отрицательна, то на этом
интервале функция ![]() будет убывающей, т. е.
будет убывающей, т. е.
![]() (6)
(6)
Доказательство: 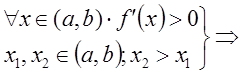 по
теореме Логранжа
по
теореме Логранжа ![]()
![]()
![]()
![]() . Аналогично
доказывается и условие (6).
. Аналогично
доказывается и условие (6).
Определение: дельта
окрестностей точки ![]() называется интервал
называется интервал ![]()
![]() , где
, где ![]() .
.
Определение: функция ![]() имеет максимум в т.
имеет максимум в т. ![]() , если существует такая
, если существует такая ![]() окрестность
окрестность ![]() , что
для всех точек этой окрестности за исключением точки
, что
для всех точек этой окрестности за исключением точки ![]() выполняется
неравенство:
выполняется
неравенство: ![]() , т. е.
, т. е.
![]() - т. максимума для
- т. максимума для ![]() \
\![]() (8)
(8)
Определение: функция ![]() имеет минимум в т.
имеет минимум в т. ![]() , если существует такая
, если существует такая ![]() окрестность
окрестность ![]() , что
для всех точек этой окрестности за исключением точки
, что
для всех точек этой окрестности за исключением точки ![]() выполняется
неравенство:
выполняется
неравенство: ![]() , т. е.
, т. е.
![]() - т. минимума для
- т. минимума для ![]() \
\![]() (9)
(9)
{т. максимума или т.
минимума}![]() т. extr.
т. extr.
Определение. Точки, в которых первая производная не существует или равна нулю называются критическими.
Теорема: Необходимый признак существования экстремума.
Если непрерывная на![]() функция
функция
![]() имеет в некоторой точке
имеет в некоторой точке ![]() этого интервала экстремум, то эта точка
этого интервала экстремум, то эта точка ![]() есть критическая для функции
есть критическая для функции ![]() .
.
![]() ;
; ![]() -т. экстремума
-т. экстремума ![]() -
критическая точка (10)
-
критическая точка (10)
Обратное утверждение не верно.
Теорема: достаточный признак существования экстремума.
1. Пусть т. ![]() -
критическая для функции
-
критическая для функции ![]() . Если при переходе
через эту критическую точку слева направо производная
. Если при переходе
через эту критическую точку слева направо производная ![]() будет
менять свой знак с «+» на «-», то точка
будет
менять свой знак с «+» на «-», то точка ![]() есть
точка максимума, а если с «-» на «+», то точка
есть
точка максимума, а если с «-» на «+», то точка ![]() есть
точка минимума. Если знак производной не меняется, то в точке
есть
точка минимума. Если знак производной не меняется, то в точке ![]() экстремума нет.
экстремума нет.
Доказательство: а).![]()
![]()
б). ![]()
![]() - точка максимума.
Аналогично доказывается и для точки минимума.
- точка максимума.
Аналогично доказывается и для точки минимума.
2. Пусть в т. ![]() первая
производная равна нулю а вторая производная существует и отлична от нуля.
Тогда,
первая
производная равна нулю а вторая производная существует и отлична от нуля.
Тогда, ![]() , таким образов в точке
, таким образов в точке ![]() будет максимум, если
будет максимум, если ![]() - то минимум, т. е.
- то минимум, т. е.
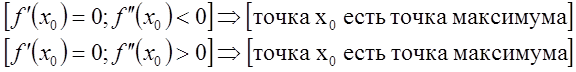 (11)
(11)
Доказательство: 1. ![]()
2. 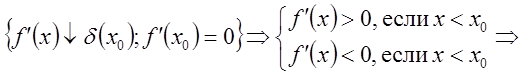 т.
т. ![]() - мах
- мах
3. Пусть ![]() ;
; ![]() ;
; ![]() . Если
n-четное, то в точке
. Если
n-четное, то в точке ![]() экстремум
есть, причем точка максимума, если
экстремум
есть, причем точка максимума, если ![]() , и точка минимума,
если
, и точка минимума,
если ![]() . Если же
. Если же ![]() -
нечетное, то в точке
-
нечетное, то в точке ![]() экстремума нет.
экстремума нет.
Непрерывная на отрезке ![]() функция
функция
![]() будет достигать своего наибольшего и
наименьшего значения или на границах этого отрезка, или же во внутренних
критических точках.
будет достигать своего наибольшего и
наименьшего значения или на границах этого отрезка, или же во внутренних
критических точках.
Пример 1. Исследовать на экстремум функции. 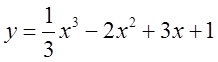 . Найти интервалы монотонности функции и
точки экстремума.
. Найти интервалы монотонности функции и
точки экстремума.
![]() ;
; ![]() ;
; ![]()
![]() ;
; ![]()
![]() .
.
|
|
|
|
1 |
|
3 |
|
|
|
|
|
7/3 |
|
1 |
|
||
|
|
+ |
0 |
- |
0 |
+ |
Пример 2. Найти наибольшее и наименьшее значение функции ![]() на отрезке [-1;
2]. Решение:
на отрезке [-1;
2]. Решение: ![]() ;
; ![]()
![]()
![]() ;
; ![]() .
.
|
|
-1 |
1 |
2 |
|
|
2 |
-2 |
2 |
Пример 3. Найти высоту цилиндра наибольшего объема, который можно вписать в данный прямой конус.
Решение:
1. ![]()
![]() .
.
2. 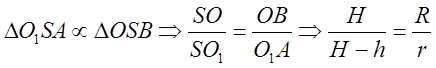
![]()
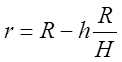
3. 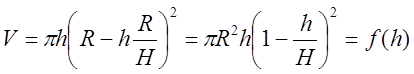
4. 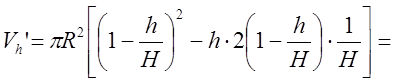
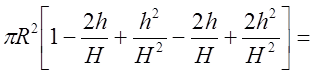
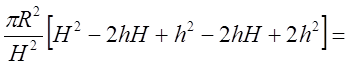
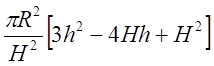
5. ![]() ;
; 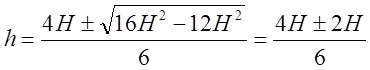
![]() ;
; 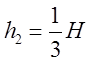
6. 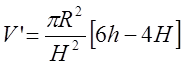 ;
; 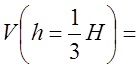
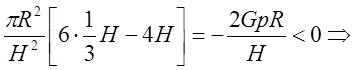 т.
т. 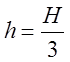 -
есть точка максимума.
-
есть точка максимума.
Ответ: 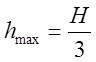 ;
; 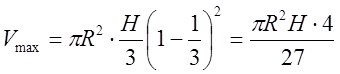
Определение: график дифференцируемой
функции ![]() называется выпуклым на интервале
называется выпуклым на интервале ![]() , если он расположен ниже любой своей
касательной, расположенной на этом интервале.
, если он расположен ниже любой своей
касательной, расположенной на этом интервале.
Определение: график дифференцируемой
функции ![]() называется вогнутым на интервале
называется вогнутым на интервале ![]() , если он расположен ниже любой своей
касательной, расположенной на этом интервале.
, если он расположен ниже любой своей
касательной, расположенной на этом интервале.
Определение: точки, в которых график меняет характер выпуклости, называются точками перегиба.
Определение: точки, в которых вторая производная равна нулю или вообще не существует, называются критическими точками II-го рода.
Теорема о достаточном признаке
выпуклости и вогнутости. Пусть функция ![]() имеет
вторую производную
имеет
вторую производную ![]() во всех точках интервала
во всех точках интервала ![]() . Если во всех точках интервала
. Если во всех точках интервала ![]() , то график функции в этом интервале
выпуклый, если же
, то график функции в этом интервале
выпуклый, если же ![]() - то вогнутый, т. е.
- то вогнутый, т. е.
![]() - выпукла на
- выпукла на ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.