![]() первые
первые ![]() -уравнений линейно-независимы, а остальные
-уравнений линейно-независимы, а остальные ![]() уравнений линейно выражаются через первые.
Имеем систему:
уравнений линейно выражаются через первые.
Имеем систему:
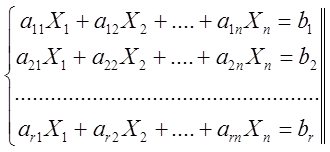
![]() а)
а)![]()

![]() по формулам Крамера:
по формулам Крамера:
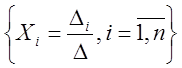 -единственное решение.
-единственное решение.
б). ![]()
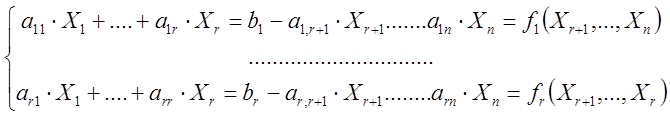
![]() -свободные переменные.
-свободные переменные.
![]() ,
,![]()
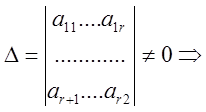 по формулам Крамера:
по формулам Крамера: 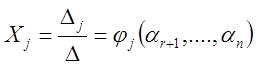 ,
,![]()
Имеем бесчисленное кол-во решений: 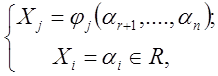
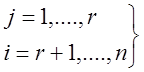
Что и требовалось доказать.
Опр. Если 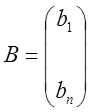
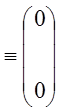 ,
то система
,
то система 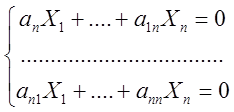 называется однородной.
называется однородной.
Эта система всегда совместна, т.к. по крайней мере одно тривиальное решение
![]() ,
,![]()
Теорема. Для того, чтобы однородная система имела нулевое решение, необходимо и
достаточно, чтобы главный определитель системы был равен нулю.
Д-во. а)Необходимость. Пусть система имеет нулевое
решение. Докажем что в этом случае ![]() Действительно, если
допустить противное, т.е.
Действительно, если
допустить противное, т.е. ![]() , то по формулам
Крамера:
, то по формулам
Крамера: 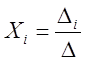 ,
, ![]() Но
Но 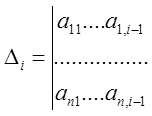
![]()
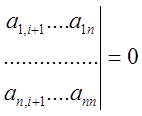 ,
,
![]() имеется только одно нулевое решение, что
противоречит условию.
имеется только одно нулевое решение, что
противоречит условию.
б) Достаточность. Пусть ![]() Тогда
Тогда ![]() Кроме того,
Кроме того, ![]() , т.к.
последний столбец расширенной матрицы
, т.к.
последний столбец расширенной матрицы ![]() -нулевой.
Имеем
-нулевой.
Имеем![]() имеем бесчисленное кол-во решений, среди
которых существуют и ненулевые.
имеем бесчисленное кол-во решений, среди
которых существуют и ненулевые.
------------------------------ разрыв страницы à конец страницы 12 -------------
------------------------------ разрыв страницы à начало страницы 17 -------------
Для пространства базис ![]() Т.А
Т.А![]() начало. Т.В
начало. Т.В ![]() конец
вектора.
конец
вектора.
![]()
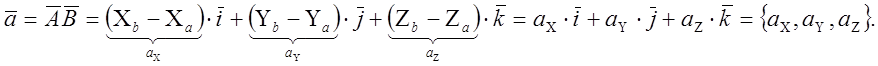
![]()
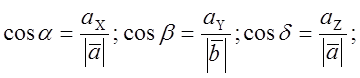
![]()
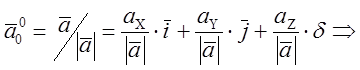
![]()
Направление вектора ![]() задается
единичным вектором
задается
единичным вектором ![]() , координатами которого служат
направляющие косинусы.
, координатами которого служат
направляющие косинусы.
![]() Пример.
Пример. 
![]() Разделить
отрезок М1 М2 , проходящий через т. М1
(X1, Y1, Z1) и
М2 (X2, Y2,
Z2) в заданном
Разделить
отрезок М1 М2 , проходящий через т. М1
(X1, Y1, Z1) и
М2 (X2, Y2,
Z2) в заданном 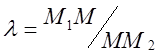 Решение.
Решение.
1)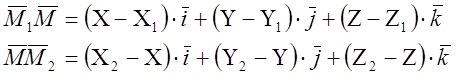
![]()
![]() 2)
2)![]()
![]()
![]() =
=![]()
![]()
![]()
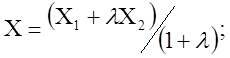
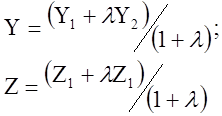
В частности, если ![]() (деление отрезка пополам, то
(деление отрезка пополам, то 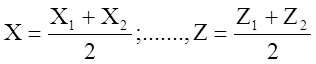
Определение Скалярным
произведением двух векторов ![]() называют число, равное
произведению модулей этих векторов на косинус угла между ними.
называют число, равное
произведению модулей этих векторов на косинус угла между ними. ![]()
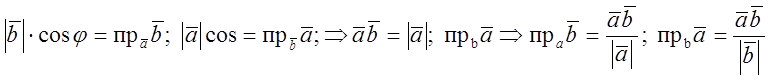
Свойства. 1) Скалярное произведение коммутативно, ассоциативно и дистрибутивно:
![]()
2)![]() Скалярный квадрат вектора
Скалярный квадрат вектора
равен квадрату его модуля.
3) Теорема
Для того чтобы два ненулевых вектора ![]() были перпендикулярными,
были перпендикулярными,
необходимо и достаточно, чтобы их скалярное произведение равно нулю.
![]()
Доказательство. Необходимость.![]()
Достаточность. ![]()
Выражение скалярного произведения через проекции перемноженных векторов.
![]()
![]()
![]()
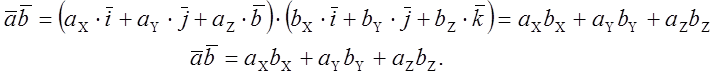
Условие перпендикулярности
двух векторов: ![]()
Угол между векторами: 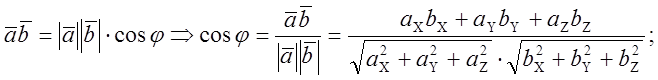
Физическое приложение. Если вектор ![]() изображает
силу, точка приложения которой
изображает
силу, точка приложения которой
перемещается из начала в
конец вектора ![]() , то работа А этой силы
определяется равенством:
, то работа А этой силы
определяется равенством: ![]()
Определение Векторным
произведением вектора ![]() на вектор
на вектор ![]() называют
вектор
называют
вектор ![]() , удовлетворяющий следующим условиям: 1)его модуль равен площади параллелограмма, построенного на
векторах
, удовлетворяющий следующим условиям: 1)его модуль равен площади параллелограмма, построенного на
векторах ![]() как на сторонах:
как на сторонах: ![]()
2) Вектор ![]() перпендикулярен площади
перпендикулярен площади ![]() , в которой лежат векторы сомножители.
, в которой лежат векторы сомножители.
(а значит ![]() и самими векторами
и самими векторами ![]() ):
):![]()
3) если смотреть с конца вектора ![]() ,
то кратчайший поворот от вектора
,
то кратчайший поворот от вектора ![]() до вектора
до вектора![]()
осуществляется против часовой стрелки.
Свойства. 1) Векторное произведение не коммутативно: ![]() .
.
2) Векторное произведение ассоциативно и дистрибутивно:
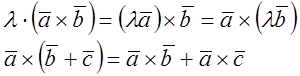
3)Теорема. Для того, чтобы два ненулевых вектора были коллинеарными, необходимо
и достаточно, чтобы их векторное произведение равнялось нулю.
![]()
![]()
![]()
![]()
![]()
![]()
![]() Доказательство. 1)Необходимость:
Доказательство. 1)Необходимость: ![]()
2)Достаточность: ![]()
Следствие. ![]()
![]()
![]() .
.
![]()
![]()
Заметим, что:

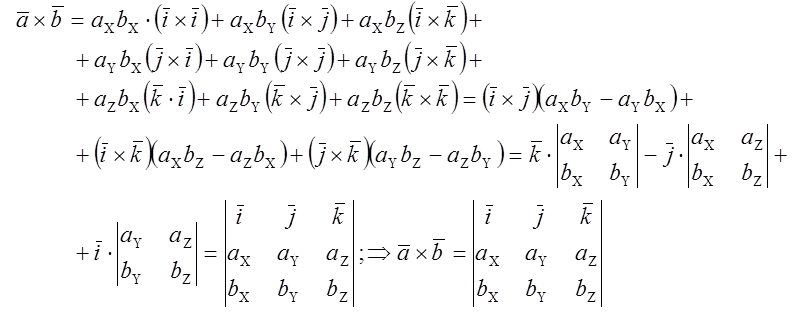
![]()
![]() Условие каллинеарности векторов:
Условие каллинеарности векторов: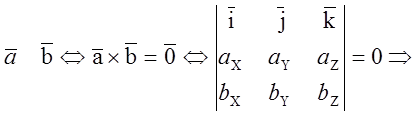
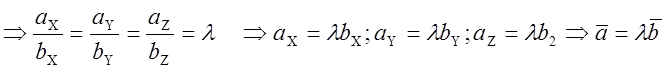
Физическое приложение. 1) Если вектор ![]() изображает силу, приложенную к точке
изображает силу, приложенную к точке![]() а вектор
а вектор ![]() идет из
некоторой точки О в точку N, то вектор
идет из
некоторой точки О в точку N, то вектор ![]() представляет собой момент силы
представляет собой момент силы
![]() относительно точки О.
относительно точки О.
2) Если ![]() вектор угловой
скорости,
вектор угловой
скорости, ![]() радиус вектор произвольной точки N, то ее линейная скорость есть:
радиус вектор произвольной точки N, то ее линейная скорость есть:![]()
Определение Смешанным
произведением трех векторов ![]() называют число, равное
скалярному произведению вектора
называют число, равное
скалярному произведению вектора ![]() на вектор
на вектор ![]() .
.
Имеем:1) ![]()
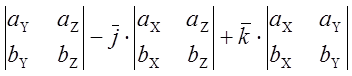
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.