Определение.
Производной функции ![]() в точке
в точке ![]() называется
предел отношения приращения функции
называется
предел отношения приращения функции ![]() в этой точке к
вызвавшему это приращение приращению аргумента
в этой точке к
вызвавшему это приращение приращению аргумента ![]() при
условии, что приращение стремится к нулю:
при
условии, что приращение стремится к нулю:
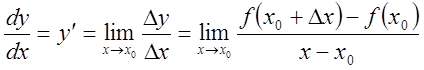 (1)
(1)
Вывод: 1)Скорость
![]() прямолинейного движения материальной точки
в момент времени
прямолинейного движения материальной точки
в момент времени ![]() есть производная от пути
есть производная от пути ![]() по времени
по времени ![]() .
.
2)Угловой
коэффициент касательной к графику функции в точке ![]() равен
значению производной этой функции в этой точке.
равен
значению производной этой функции в этой точке.
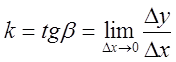 (2)
(2)
Пример. Найти производную функции ![]() в точке
в точке
![]() .
.
Решение. ![]()
![]()
![]()
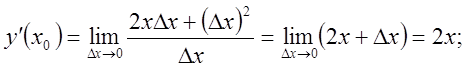
![]()
Определение. Если
функция имеет производную в точке ![]() , то она называется
дифференцируемой в этой точке.
, то она называется
дифференцируемой в этой точке.
Теорема . Если функция ![]() -дифференцируемая в точке
-дифференцируемая в точке![]() , то она в этой точке непрерывна.(обратно
не верно)
, то она в этой точке непрерывна.(обратно
не верно)
Доказательство.
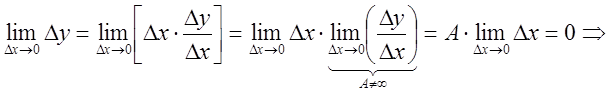 функция непрерывна в точке
функция непрерывна в точке ![]() .
.
Пример
обратного: ![]()
![]() в точке
в точке ![]() .
.
1).
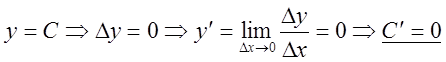 .
.
2).![]()
![]()
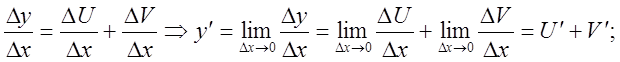
Итак:![]()
3).![]()
![]()
![]()
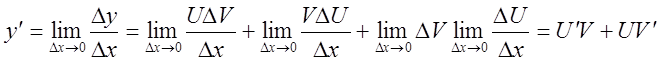
Итак:![]()
4).
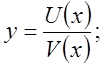
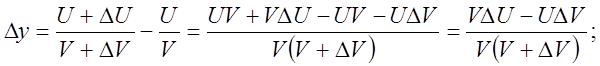
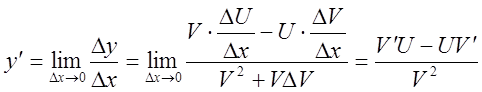
Итак: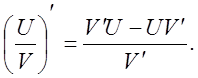
5).![]()
![]()
![]()
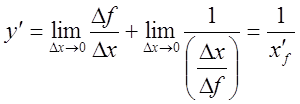 Итак:
Итак: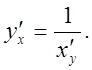
6).![]()
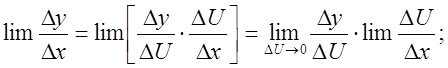
![]()
1).![]()
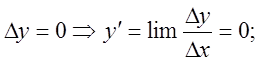
![]()
2).![]()
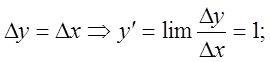
![]()
3).![]()
![]()
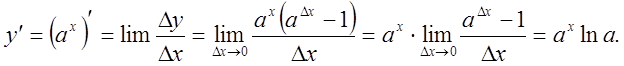
![]()
![]()
4).![]()
![]()
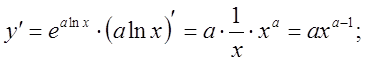
5).![]()
![]()
![]()
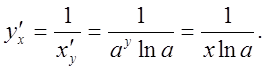
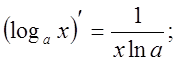
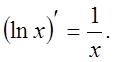
6).![]()
![]()
![]()
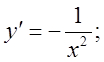
![]()
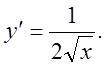
7).![]()
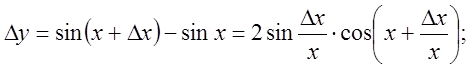
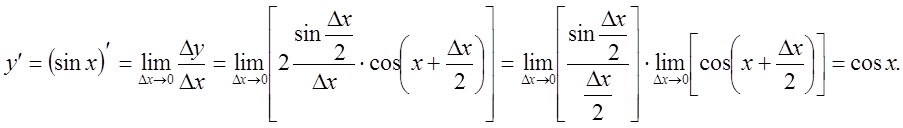
![]()
![]()
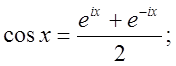
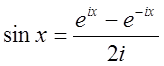 где
где ![]()
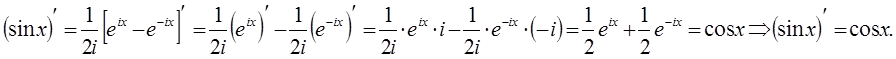
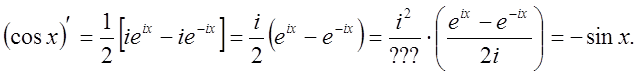
8).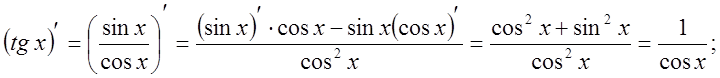
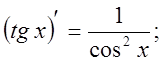
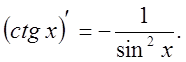
9).![]()
![]()
![]()
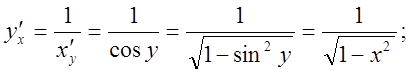
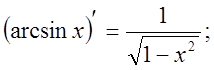
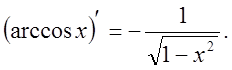
10).![]()
![]()
![]()
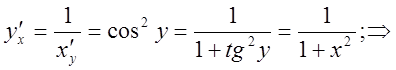
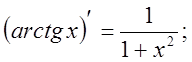
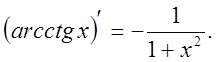
11).Производные гиперболических функций.
![]()
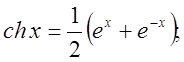
![]() ??????
??????
![]()
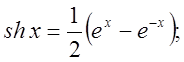
![]() ??????
??????
![]()
![]()
![]()
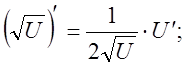
![]()
![]()
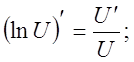
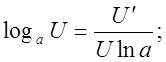
![]()
![]()
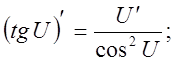
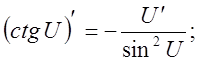
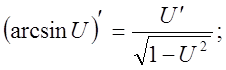
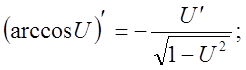
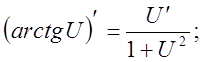
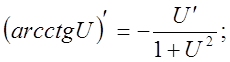
![]()
![]()
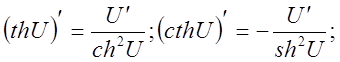
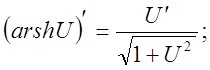
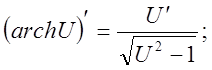
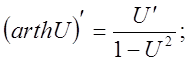
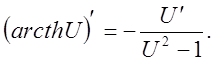
Логарифмическое дифференцирования и дифференцирование неявно заданных функций.
1.
![]()
![]()
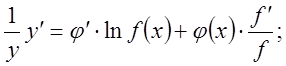
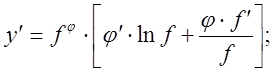 Пр.
Пр. ![]()
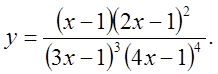
2.
![]() -
неявно заданная функция. а)
-
неявно заданная функция. а)
![]()
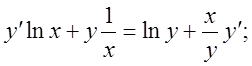
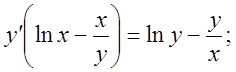
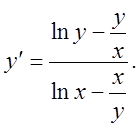 б)
б) ![]()
![]()
![]()
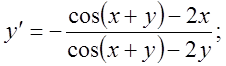
![]() :Опр. Нормалью к кривой в точке
:Опр. Нормалью к кривой в точке ![]() называют перпендикуляр к касательной,
проведённый через точку касания.
называют перпендикуляр к касательной,
проведённый через точку касания.
![]() :
:![]()
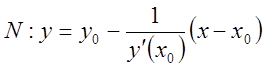
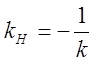
![]()
Пример. 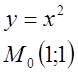
![]()
Пример: ![]() ;
; ![]() ;
; ![]() -
линейная часть.
-
линейная часть. ![]()
Определение: говорят, что функция ![]() имеет дифференциал в точке х0,
если в этой точке ее приращение
имеет дифференциал в точке х0,
если в этой точке ее приращение ![]() может быть записано в
следующем виде:
может быть записано в
следующем виде:
![]() (1)
(1)
где ![]() - главная часть
приращения функции, линейная, относительно приращения ее аргумента.
- главная часть
приращения функции, линейная, относительно приращения ее аргумента.![]() - бесконечно малая более высокого порядка, чем
- бесконечно малая более высокого порядка, чем ![]() , т. е.
, т. е. 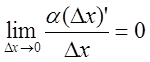 (2)
(2)
Определение: в этом случае главная часть
приращения функции, линейная относительно приращения своего аргумента,
называется дифференциалом и обозначается ![]() , т. е.
, т. е.
![]() .
.
Теорема: Если функция ![]() имеет в точке
имеет в точке ![]() дифференциал,
то в этой точке функция дифференцируема.
дифференциал,
то в этой точке функция дифференцируема.
Доказательство: 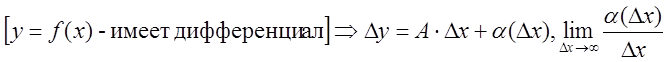
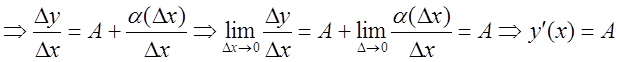 .
.
Следствие: ![]()
Теорема:
Если в некоторой точке ![]() функция дифференцируема, то в
этой точке она имеет дифференциал.
функция дифференцируема, то в
этой точке она имеет дифференциал.
Доказательство: 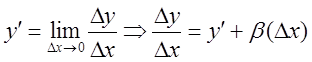 , где
, где
![]()
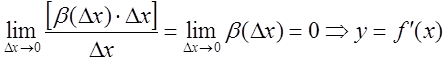 - имеет дифференциал.
- имеет дифференциал.
Пример: ![]() ;
; ![]() ;
; ![]() .
.
Вывод.
Дифференциал независимой переменной равен ее приращению ![]() ;
;
![]()
![]() .
. ![]()
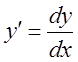 .
.
Вывод: Дифференциал функции равен произведению производной функции на дифференциал независимой переменной.
Свойства:
![]() ;
; ![]() ;
; 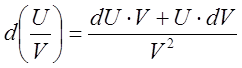 .
.
1)
![]() ;
; ![]() -независимая переменная.
-независимая переменная. ![]()
2)
![]() ,
, ![]() ;
; ![]() -
независимая переменная,
-
независимая переменная, ![]() -промежуточный аргумент.
-промежуточный аргумент.
![]() ;
; 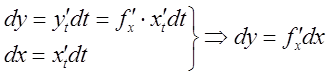 .
.
Вывод – дифференциал функции ![]() не
зависит от того, будет ли аргумент
не
зависит от того, будет ли аргумент ![]() неизвестной переменной
или же будет являться в свою очереди некоторой функцией новой переменной
неизвестной переменной
или же будет являться в свою очереди некоторой функцией новой переменной ![]() (свойство инвариантности формы I-го
дифференциала).
(свойство инвариантности формы I-го
дифференциала).
Определение: дифференциалом ![]() -ого порядка (
-ого порядка (![]() -ым
дифференциалом) функции
-ым
дифференциалом) функции ![]() называют дифференциал
от ее
называют дифференциал
от ее ![]() -ю дифференциала.
-ю дифференциала.
![]()
Пусть х – независимая переменная. ![]() ,
, ![]()
![]()
![]() ,
аналогично
,
аналогично ![]()
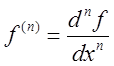 .
.
Из ![]()
Вывод: дифференциал геометрически представляет собой
приращение ординаты касательной , проведенной к графику функции в базовой точке
![]() .
.
Это используется для приблизительных вычислений:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.