Задача:
Через заданную точку ![]() провести плоскость
провести плоскость ![]() , перпендикулярную заданному вектору
, перпендикулярную заданному вектору ![]() .
.
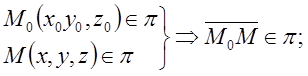
![]()
![]()
![]()
![]() (1) – уравнение плоскости, проходящей
через заданную точку
(1) – уравнение плоскости, проходящей
через заданную точку ![]() перпендикулярно заданному
вектору
перпендикулярно заданному
вектору ![]() .
.
Вывод: Всякая плоскость описывается уравнением первой степени относительно текущих координат.
Обратно: Всякое уравнение I-ой степени относительно переменных, будет представлять в пространстве некоторую плоскость.
![]() (2)
(2) ![]() Пусть
Пусть ![]()
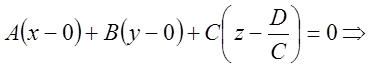 Плоскость проходит
через т.
Плоскость проходит
через т.![]() перпендикулярно вектору
перпендикулярно вектору ![]() .
.
Уравнение (2) называют уравнением плоскости в общем виде.
Для
построение плоскости удобно использовать уравнение плоскости в отрезках: 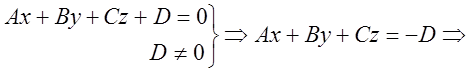
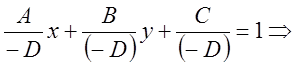
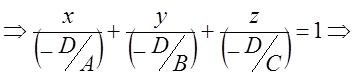
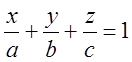 - уравнение плоскости в отрезках, где
- уравнение плоскости в отрезках, где ![]() ;
; ![]() ;
; ![]() .
.
Пример
1. Составить уравнение плоскости ![]() , проходящей через три
заданные точки
, проходящей через три
заданные точки ![]() ,
, ![]() ,
, ![]() .
.
Решение.
1)
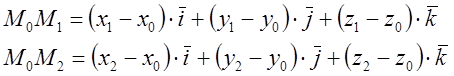
2)
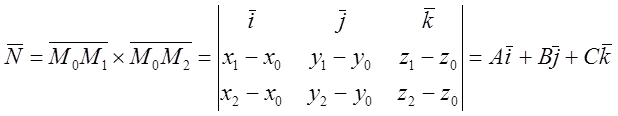 , где
, где
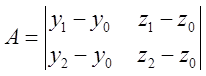 ;
; 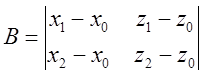 ;
; 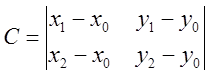
3)
![]()
4)
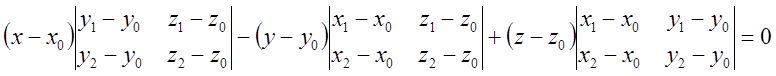
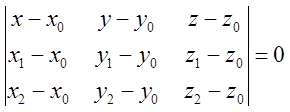 - уравнение
плоскости, проходящей через три точки.
- уравнение
плоскости, проходящей через три точки.
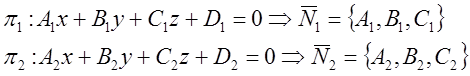
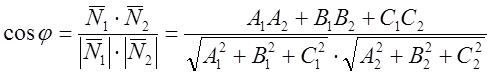
А) ![]()
![]() - условие перпендикулярности двух плоскостей.
- условие перпендикулярности двух плоскостей.
Б) ![]()
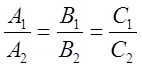 - условие
параллельности двух плоскостей.
- условие
параллельности двух плоскостей.
Пример
№2. Составить уравнение плоскости ![]() , проходящей через
заданную точку
, проходящей через
заданную точку ![]() , параллельно заданной плоскости
, параллельно заданной плоскости ![]() .
.
Решение.
![]()
![]()
![]() - уравнение плоскости. Проходящей через
заданную точку || заданной
плоскости.
- уравнение плоскости. Проходящей через
заданную точку || заданной
плоскости.
Пример №3. Составить уравнение плоскости ![]() , проходящей через заданную точку
, проходящей через заданную точку ![]() перпендикулярно плоскостям
перпендикулярно плоскостям 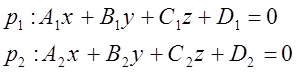 .
.
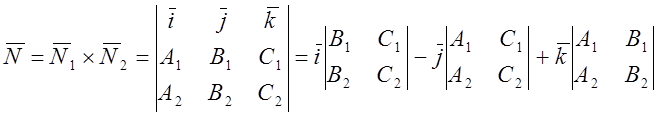
![]() ;
;
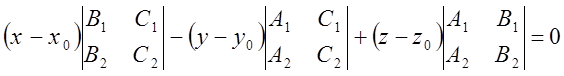 ;
; 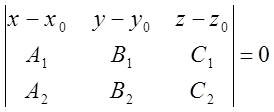 - уравнение плоскости, проходящей через т.
- уравнение плоскости, проходящей через т.![]() перпендикулярно плоскостям
перпендикулярно плоскостям ![]() и
и ![]() .
.
Пример
№4. Составить уравнение плоскости, проходящей через т. ![]() и
и ![]() перпендикулярно плоскости
перпендикулярно плоскости ![]() .
.
Решение.
![]() ;
; ![]()
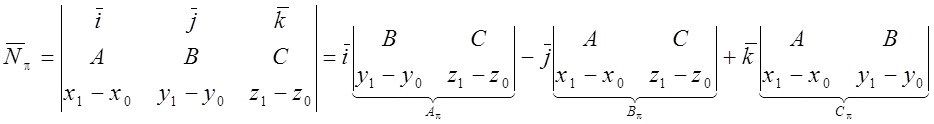
![]()
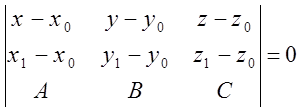 - уравнение
плоскости, проходящей через т.
- уравнение
плоскости, проходящей через т. ![]() и
и ![]() перпендикулярно к плоскости
перпендикулярно к плоскости ![]() .
.
![]() ,
, ![]()
1.
![]() ;
; ![]()
2.
![]()
![]()
3.
![]()
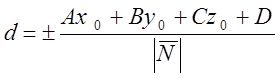 ;
; 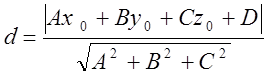
![]()
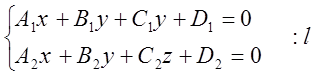 - общее уравнение прямой.
- общее уравнение прямой. ![]()
Примечание. Для построения прямой, заданной общим уравнением, удобно использовать точки пересечения этой прямой с координатными плоскостями.
Определение.
Вектор ![]() , указывающий направление прямой
, указывающий направление прямой ![]() в пространстве, называют ее направляющим
вектором.
в пространстве, называют ее направляющим
вектором.
Задача.
Через заданную точку ![]() провести прямую
провести прямую ![]() параллельно заданному вектору
параллельно заданному вектору ![]() .
.
Решение.
![]()
![]() ;
; ![]() ,
, ![]() -параметр.
-параметр.
![]()
![]()
![]()
![]() - векторное уравнение прямой в
пространстве.
- векторное уравнение прямой в
пространстве.
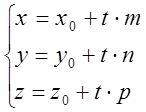 - параметрическое уравнение прямой
- параметрическое уравнение прямой ![]()
![]()
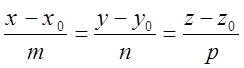 -
каноническое уравнение прямой, проходящей через заданную т.
-
каноническое уравнение прямой, проходящей через заданную т. ![]() параллельно вектору
параллельно вектору ![]() .
.
Переход
от канонического задания 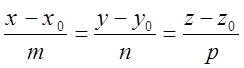
![]()
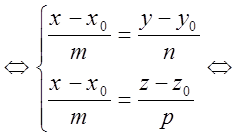
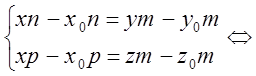
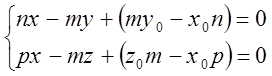
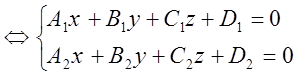
Переход от общего вида к каноническому:
1.
Имеем 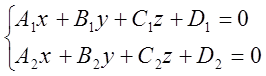
2.
Находим одну из точек прямой ![]() , например точку пересечения с плоскостью
, например точку пересечения с плоскостью ![]() :
:
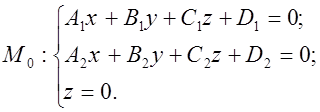
![]()
3.
Находим направляющий вектор ![]() , в качестве которого выбираем
, в качестве которого выбираем ![]()
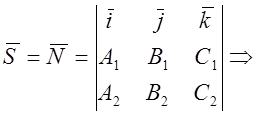
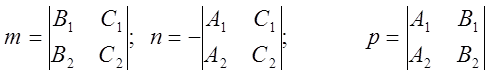
4.
Записываем каноническое уравнение ![]()
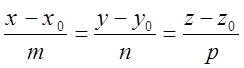 .
.
В качестве направляющего вектора ![]() выбираем вектор
выбираем вектор ![]() .
Имеем:
.
Имеем: ![]()
![]() ;
; ![]() .
.
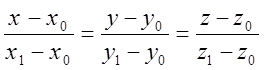 - уравнение прямой,
проходящей через две заданные точки.
- уравнение прямой,
проходящей через две заданные точки.
Определяется углом между их направляющими векторами:
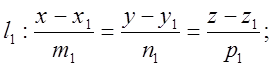
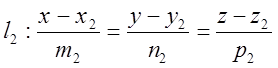
![]()
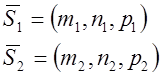
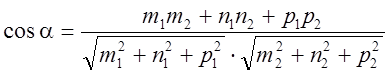 ;
;
Условие 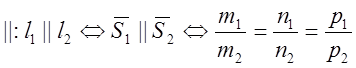 .
.
Условие ![]() .
.
1. Условие параллельности и перпендикулярности.
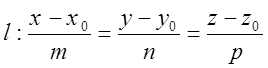 ;
; ![]() ;
; 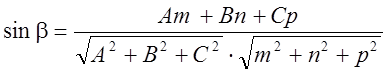 .
.
А) ![]()
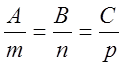
Б) ![]()
![]()
2.
Точка пересечения прямой с
плоскостью ![]()
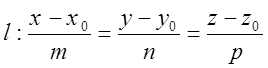 ;
; ![]() .
.
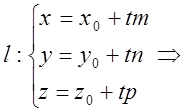
![]()
![]()
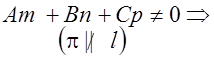
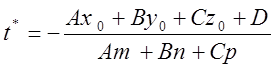
![]()
![]() ;
; ![]() ;
; ![]() .
.
Пример
№1. Найти уравнение плоскости, проходящей через прямую 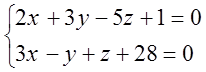 и
точку
и
точку ![]() .
.
Решение.
1.
Запишем уравнение пучка
плоскостей, проходящих через данную прямую: ![]() .
.
2.
Подставим в полученное уравнение
координаты т. ![]() :
: ![]()
![]() .
.
3.
Подставляем найденное значение ![]() в уравнение пучка:
в уравнение пучка: 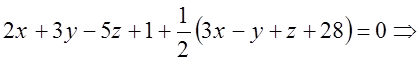
![]() .
.
Пример
№2. Вычислить расстояние ![]() от т.
от т.![]() до прямой
до прямой 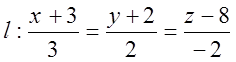 .
.
![]() (-3; -2; 8)
(-3; -2; 8) ![]()
![]() (3; 2; -2) направляющий
вектор
(3; 2; -2) направляющий
вектор ![]()
![]() =
=![]()
![]()
 ;
; ![]() =S---; S---=
=S---; S---=
![]()
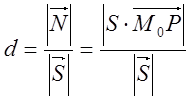
Имеем: 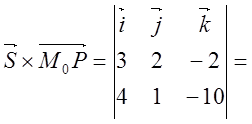 -18
-18![]() +22
+22![]() -5
-5![]()
![]()
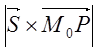 =
=![]() .
.
Пример 3. Вычислить кратчайшее расстояние между прямыми:
L1: 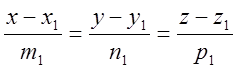 ; L2:
; L2: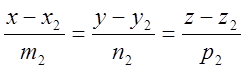
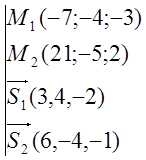
Решение. 1.Строим плоскость, проходящую через прямую l1 параллельно прямой l2.
![]()
П: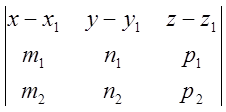 =0.
=0. ![]() Ax+By+Cz+D=0
:П
Ax+By+Cz+D=0
:П
2. Находим расстояние от т. ![]() до плоскости П :
до плоскости П : 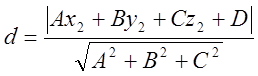 ;
;
2-ой подход: 1.Находим объём параллелепипеда,
построенного на векторах![]() ,
,![]() и
и![]() : V=
: V=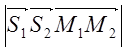
2.Находим площадь
основания: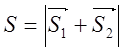
3.Имеем ![]()
![]()
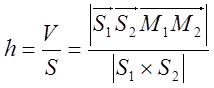
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.