Приклади розв'язання задач до контрольної роботи № 6
Задача 1. Знайти
область збіжності функціонального ряду 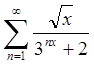 .
.
Розв'язання.Очевидно, маємо ряд з додатними членами, причому ![]() .
.
Застосуємо ознаку Даламбера, враховуючи, що ![]() .
.
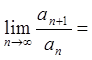
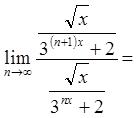
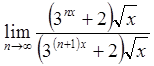
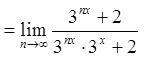
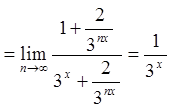 .
.
Ряд збігається, якщо 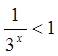 . Ця нерівність,
очевидно, виконується для будь – яких
. Ця нерівність,
очевидно, виконується для будь – яких ![]() .
.
Таким чином, область збіжності даного ряду є інтервал ![]() .
.
Задача 2. Знайти
область збіжності функціонального ряду 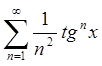 .
.
Розв'язання.Очевидно, 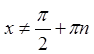 ,
, ![]() .
.
Розглянемо ряд 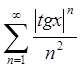 , складений з абсолютних
величин членів даного ряду. Застосуємо до цього ряду радикальну ознаку Коші
, складений з абсолютних
величин членів даного ряду. Застосуємо до цього ряду радикальну ознаку Коші
![]()
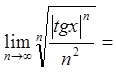
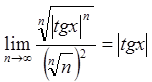 .
.
Ряд збігається, якщо ![]() . Звідси
. Звідси 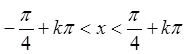 ,
, ![]() .
.
Ряд 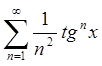 абсолютно збігається при
абсолютно збігається при 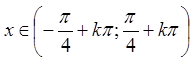 ,
, ![]() .
.
Перевіримо виконання необхідної умови збіжності даного ряду, якщо ![]() , тобто при
, тобто при 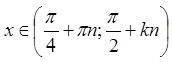 , або
, або 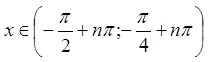 .
.
В першому випадку маємо знакододатний
ряд, в другому – знакопочередний. В обох випадках 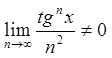 , бо
, бо
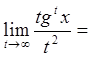
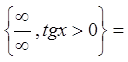
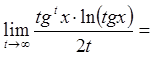
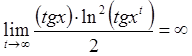 .
.
Тобто ряд 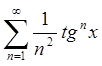 при
при 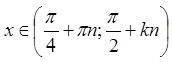 і
і 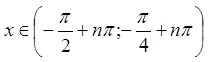 розбігається.
розбігається.
Дослідимо збіжність ряду при 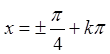 .
.
При 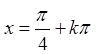 маємо
ряд
маємо
ряд 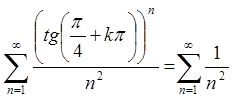 . Це узагальнений гармонічний ряд з
показником степені більшим за 1, тому він збігається.
. Це узагальнений гармонічний ряд з
показником степені більшим за 1, тому він збігається.
При 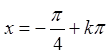 маємо
ряд
маємо
ряд 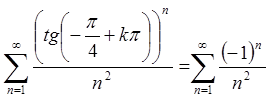 . Цей ряд абсолютно збігається, бо
збігається ряд
. Цей ряд абсолютно збігається, бо
збігається ряд 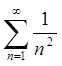 .
.
Таким чином ряд 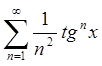 збігається, причому абсолютно, при
збігається, причому абсолютно, при 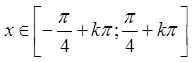 ,
, ![]() .
.
Задача 3. Знайти
область збіжності функціонального ряду 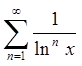 .
.
Розв'язання.Очевидно, 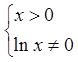
![]()
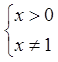 .
.
1. При ![]()
![]() і тому маємо ряд з
додатними членами. Застосуємо радикальну ознаку Коші
і тому маємо ряд з
додатними членами. Застосуємо радикальну ознаку Коші
![]()
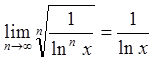 .
.
Ряд
збігається, якщо 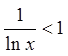
![]()
![]()
![]()
![]() ,
тобто ряд збігається при
,
тобто ряд збігається при ![]() .
.
При
![]() маємо ряд
маємо ряд 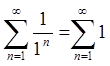 , що
розбігається, оскільки
, що
розбігається, оскільки ![]() .
.
2. При ![]()
![]() і тому маємо знакопочередний ряд.
і тому маємо знакопочередний ряд.
а) Нехай 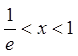 , тоді
, тоді ![]()
![]()
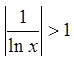 і
і 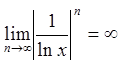 . Це означає, що ряд розбігається, бо не
виконується необхідна ознака збіжності.
. Це означає, що ряд розбігається, бо не
виконується необхідна ознака збіжності.
б) Нехай 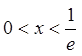 , тоді
, тоді ![]()
![]()
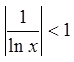 і
і 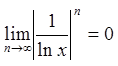 . Очевидно також
. Очевидно також 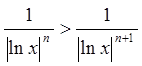 .
За ознакою Лейбніца ряд збігається. При
.
За ознакою Лейбніца ряд збігається. При 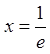 маємо
ряд
маємо
ряд 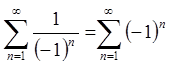 , що розбігається, оскільки
, що розбігається, оскільки ![]() .
.
Таким чином
ряд 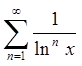 збігається при
збігається при 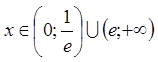 .
.
Задача 4. Знайти
область збіжності функціонального ряду 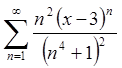 .
.
Розв'язання.Маємо степеневий ряд. За теоремою Абеля інтервал збіжності цього ряду
співпадає з інтервалом збіжності ряду 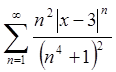 .
.
Застосуємо ознаку Даламбера
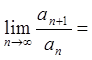
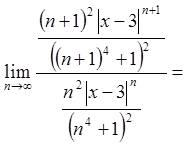
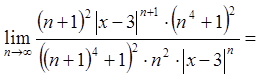
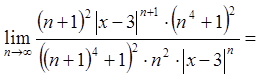
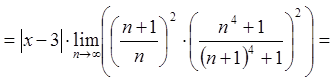
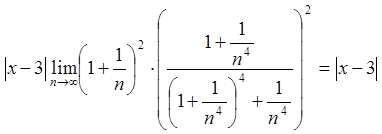 .
.
Даний ряд збігається, якщо
![]() ;
;
![]() ;
;
![]() ,
,
тобто на інтервалі: ![]() .
.
При ![]() маємо
ряд
маємо
ряд 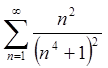 . Порівняємо його зі збіжним рядом
. Порівняємо його зі збіжним рядом 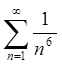 .
.
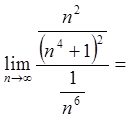
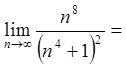
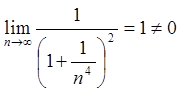 .
.
Так як значенням границі є ![]() , то ряди, в сенсі збіжності, ведуть себе
однаково. Ряд
, то ряди, в сенсі збіжності, ведуть себе
однаково. Ряд 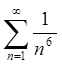 збігається, тому і ряд
збігається, тому і ряд 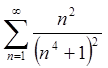 також збігається.
також збігається.
При ![]() маємо
ряд
маємо
ряд 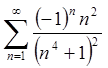 , що збігається абсолютно, бо збігається
ряд
, що збігається абсолютно, бо збігається
ряд 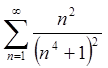 .
.
Таким чином, областю збіжності
ряду 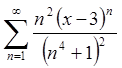 є відрізок
є відрізок ![]() .
.
Задача 5.
Довести, виходячи з означення, рівномірну збіжність функціонального ряду 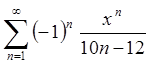 на відрізку
на відрізку ![]() . При
яких
. При
яких ![]() абсолютна величина залишкового члена ряду
не перевершує
абсолютна величина залишкового члена ряду
не перевершує ![]()
![]() ?
?
Розв'язання.Маємо знакопочередний (починаючи з другого члена) ряд. Його залишок не перевершує за абсолютною величиною першого із своїх членів, тобто
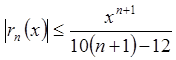 , і, очевидно
, і, очевидно 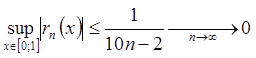 .
.
Звідси витікає, що ряд рівномірно
збігається на відрізку ![]() .
.
З’ясуємо, при яких ![]() абсолютна величина залишку ряду не
перевершує
абсолютна величина залишку ряду не
перевершує ![]() .
.
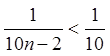
![]()
![]()
![]()
![]() .
.
Оскільки ![]() ,
то при
,
то при ![]()
![]() .
.
Задача 6. Для
даного функціонального ряду 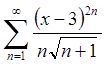 побудувати мажоруючий
ряд і довести рівномірну збіжність на відрізку
побудувати мажоруючий
ряд і довести рівномірну збіжність на відрізку ![]() .
.
Розв'язання. Очевидно, ![]() виконується нерівність
виконується нерівність
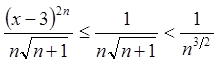 .
.
Ряд 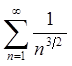 збігається
як узагальнений гармонічний ряд з показником степені більше 1. за ознакою
Вейрштраса ряд
збігається
як узагальнений гармонічний ряд з показником степені більше 1. за ознакою
Вейрштраса ряд 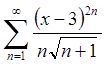 рівномірно збігається на
відрізку
рівномірно збігається на
відрізку ![]() .
.
Задача 7. Знайти
суму ряду 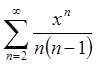 .
.
Розв'язання.Знайдемо інтервал збіжності ряду, використовуючи теорему Абеля, та радикальну ознаку Коші.
![]()
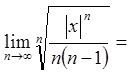
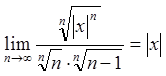 .
.
Ряд збігається при ![]() , тобто
, тобто ![]() -
інтервал збіжності ряду. В цьому інтервалі ряд збігається абсолютно і
рівномірно.
-
інтервал збіжності ряду. В цьому інтервалі ряд збігається абсолютно і
рівномірно.
Позначимо через ![]() суму ряду, тобто
суму ряду, тобто
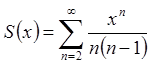 .
.
Так як ряд збігається рівномірно
на інтервалі ![]() , то його можна почленно диференціювати на
ньому (за теоремою про почленне диференціювання і інтегрування степеневого ряду
в середині інтервалу збіжності).
, то його можна почленно диференціювати на
ньому (за теоремою про почленне диференціювання і інтегрування степеневого ряду
в середині інтервалу збіжності).
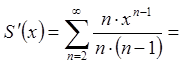
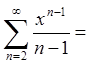
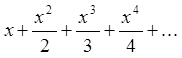 .
.
Скориставшись тим, що
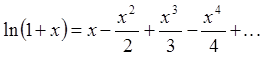 ,
,
маємо
![]() .
.
Тоді
![]()
![]()
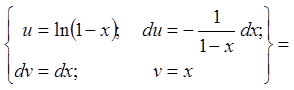
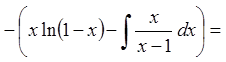
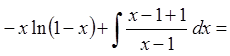
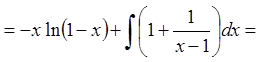
![]() . (*)
. (*)
Оскільки  ,
то із (*)
знаходимо
,
то із (*)
знаходимо
![]() .
.
Таким чином
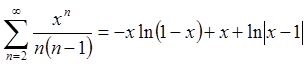 ,
, ![]() .
.
При ![]() маємо
ряд
маємо
ряд 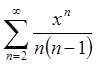 ~
~ 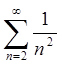 .
.
Ряд 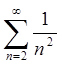 збігається,
значить і ряд
збігається,
значить і ряд 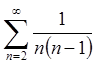 також збігається.
також збігається.
При ![]() маємо ряд
маємо ряд 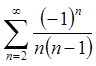 , який збігається абсолютно, оскільки збігається ряд
, який збігається абсолютно, оскільки збігається ряд 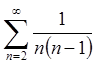 .
.
Так як ряд 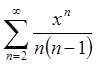 збігається на відрізку
збігається на відрізку ![]() , то його сума є неперервною функцією на
цьому відрізку.
, то його сума є неперервною функцією на
цьому відрізку.
Тому
![]()
![]()
![]()
![]()
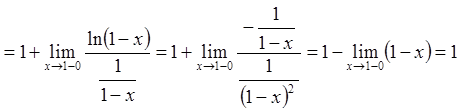 ;
;
![]()
![]() .
.
Таким чином
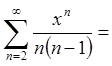
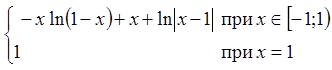 ,
,
або
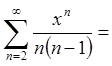
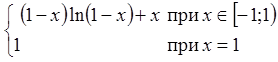 .
.
Задача 8. Знайти
суму ряду 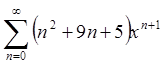 .
.
Розв'язання.Знайдемо область збіжності цього степеневого ряду. Скористаємося теорему Абеля і радикальною ознакою Коші.
![]()
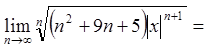
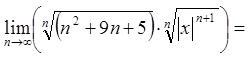
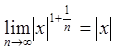 .
.
Ряд збігається при ![]() , тобто збігається абсолютно і рівномірно
на інтервалі
, тобто збігається абсолютно і рівномірно
на інтервалі ![]() .
.
При ![]() маємо
ряд
маємо
ряд 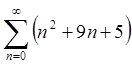 , що, очевидно, розбігається, оскільки для
нього не виконується необхідна умова збіжності:
, що, очевидно, розбігається, оскільки для
нього не виконується необхідна умова збіжності:
![]() .
.
При ![]() маємо
ряд
маємо
ряд 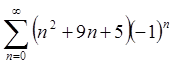 , що як і попередній ряд розбігається з
тієї ж причини.
, що як і попередній ряд розбігається з
тієї ж причини.
Таким чином ряд 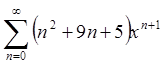 збігається абсолютно і рівномірно на
інтервалі
збігається абсолютно і рівномірно на
інтервалі ![]() .
.
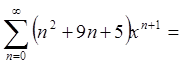
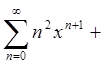
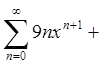
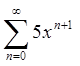 .
.
Нехай 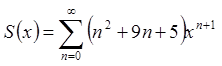 ,
, 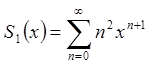 ,
, 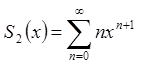 ,
, 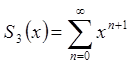 .
.
1) 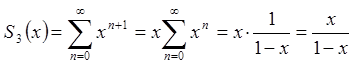 ;
;
2) 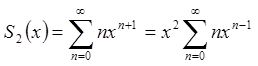 .
.
Позначимо 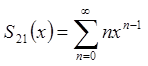 .
Проінтегруємо почленно цей ряд в інтервалі
.
Проінтегруємо почленно цей ряд в інтервалі ![]() .
.
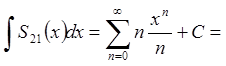
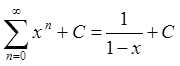 ,
,
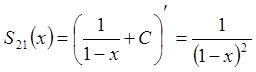 .
.
Тоді 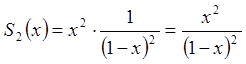 .
.
3) 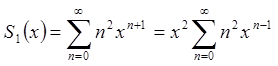 .
.
Позначимо 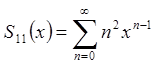 .
Проінтегруємо почленно цей ряд в інтервалі
.
Проінтегруємо почленно цей ряд в інтервалі ![]()
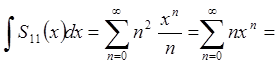
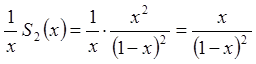 .
.
Тоді
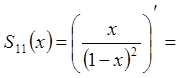
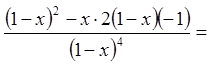
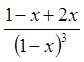
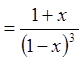 ,
,
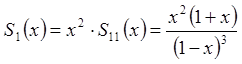 .
.
![]()
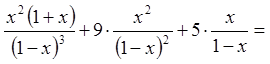
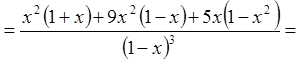
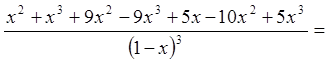
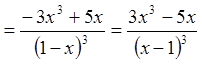 .
.
Задача 9.
Розвинути функцію 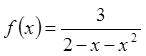 в ряд Тейлора по степеням
в ряд Тейлора по степеням ![]() .
.
Розв'язання. Запишемо функцію ![]() у вигляді суми найпростіших дробів
у вигляді суми найпростіших дробів
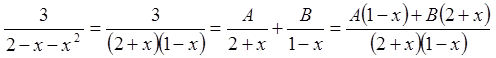 .
.
Звідси ![]() .
.
При ![]()
![]() , при
, при ![]()
![]() , маємо систему
, маємо систему
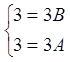
![]()
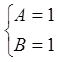 .
.
Тобто 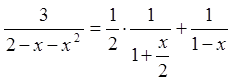 .
.
Оскільки 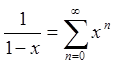 і
і
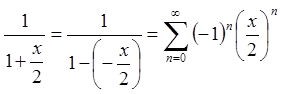 , то
, то
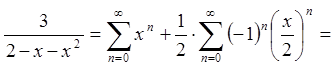
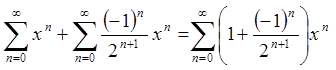 .
.
Таким чином
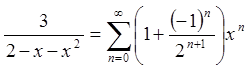 .
.
Це є ряд із додатними членами. Знайдемо його область збіжності. Скористаємося ознакою Даламбера
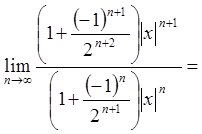
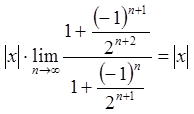 .
.
Ряд збігається при ![]() , тобто на інтервалі
, тобто на інтервалі ![]() . Дослідимо збіжність ряду на кінцях
інтервалу.
. Дослідимо збіжність ряду на кінцях
інтервалу.
При ![]() маємо
ряд
маємо
ряд 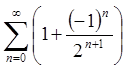 .
.
Очевидно, 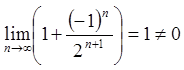 ,
тому цей ряд розбігається, оскільки не виконується необхідна умова збіжності.
,
тому цей ряд розбігається, оскільки не виконується необхідна умова збіжності.
При ![]() маємо
знакопочередний ряд
маємо
знакопочередний ряд 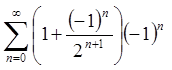 , для якого, очевидно, також не
виконується необхідна умова збіжності, тому він розбігається.
, для якого, очевидно, також не
виконується необхідна умова збіжності, тому він розбігається.
Таким чином
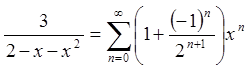 ,
, ![]() .
.
Задача 10.
Обчислити інтеграл 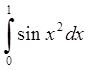 з точністю до
з точністю до ![]() .
.
Розв'язання. Запишемо відоме розвинення
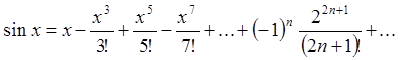 ,
, ![]() .
.
Причому цей ряд збігається
рівномірно на ![]() .
.
Тоді
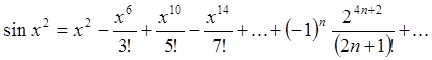 ,
, ![]() .
.
Про інтегруємо цю рівність на
відрізку ![]() .
.
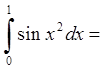
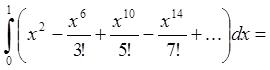
![]() {оскільки ряд під інтегралом
збігається рівномірно, то можливе почленне інтегрування}
{оскільки ряд під інтегралом
збігається рівномірно, то можливе почленне інтегрування}![]()
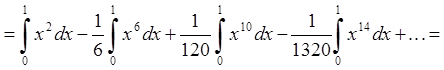
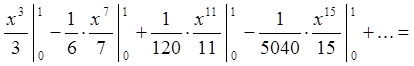
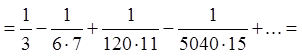
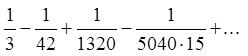
В знакопочередному ряді при заміні
його суми частиною сумою похибка за абсолютною величиною не перевищує першого з
відкинутих членів ряду. Оскільки 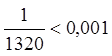 , то з точністю до
, то з точністю до ![]()
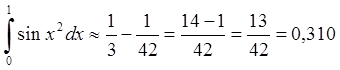 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.