Приклади розв'язання задач до контрольної роботи № 3 "Дослідження функцій і побудова їх графіків"

Приклади розв'язання задач до контрольної роботи 3

Задача 1.Знайти найбільше і найменше значення функції  на відрізку .

Розв'язання.  Очевидно, .

Знайдемо критичні точки функції.

;

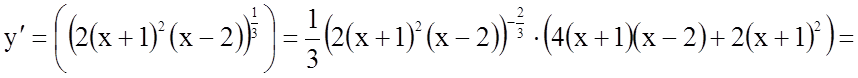
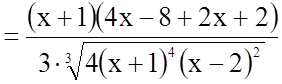
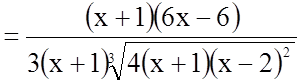
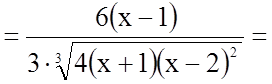
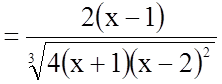а) ;  ;  ;

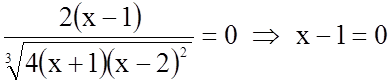б)  не існує, очевидно, при  і .

Всі критичні точки належать відрізку . Знайдемо значення функції в цих точках, а також на кінцях відрізка.

;

;

;

;

.

Таким чином,  ,  .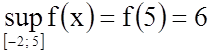

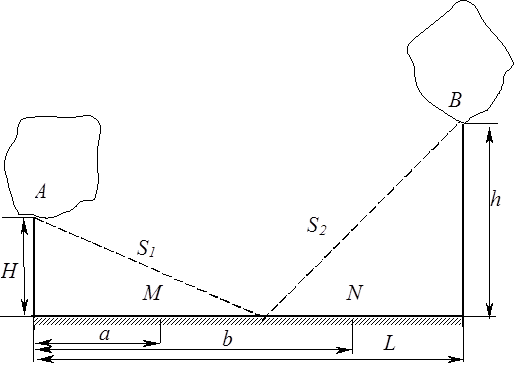Задача 2.  Рибалці треба переправитися з острова  на острів  (рис. 1). Щоб поповнити свої запаси, він повинен попасти на ділянку берега . Знайти найкоротший шлях рибалки .

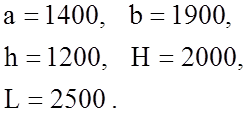
Розв'язання. Позначимо відстань від проекції точки  на лінію берега до ділянки , де повинен висадитися для поповнення своїх запасів рибалка через  .Щоб полегшити розрахунки, перейдемо до іншого масштабу, зменшивши всі відстані в 100 разів. Тоді, очевидно,  і

.

Знайдемо найменше значення функції  на відрізку .

;

      ;

;

;

;

;

.

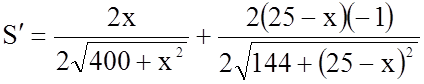
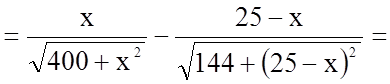
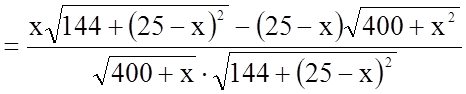Оскільки  ,  то  ;

;

;

.

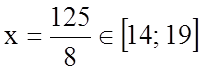Знайдемо значення функції в точці 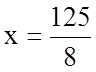 і на кінцях відрізку .

;

.

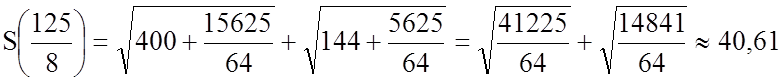
Враховуючи зміну масштабу при обчисленні, маємо, що найкоротший шлях рибалки приблизно дорівнює

.

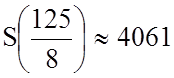Задача 3.При підготовці до екзамену студент за  днів вивчає 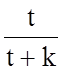-ту частину курсу, а забуває -ту частину. Скільки днів потрібно затратити на підготовку, щоб була вивчена максимальна частина курсу, якщо , а ?

Розв'язання.  Складемо функцію залежності обсягу вивченого матеріалу від кількості витрачених на вивчення цього матеріалу днів

.

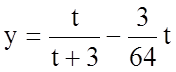Знайдемо значення , при якому ця функція досягає найбільшого значення на проміжку .

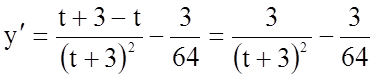,   (очевидно, ).

;   ;    ;

;   ;   .

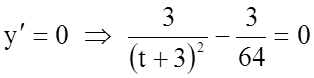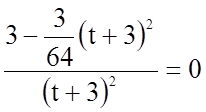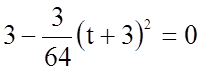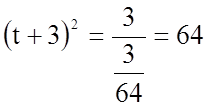За змістом задачі зрозуміло, що за 5 днів студент вивчить максимальну частину курсу.

Задача 4.  Тіло масою  кг падає з висоти  м і втрачає масу (згоряє) пропорційно часу падіння. Коефіцієнт пропорційності  кг/с. Вважаючи, що початкова швидкість , прискорення  м/с², і нехтуючи опором повітря знайти найбільшу кінетичну енергію тіла.

Розв'язання.  Формула для обчислення кінетичної енергії має вигляд

,

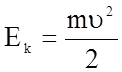а формула для обчислення швидкості  тіла, що падає – , де  – маса тіла, а  – швидкість тіла.

Очевидно, у нашому випадку в кожен момент часу

.

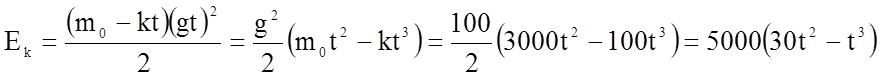Знайдемо час, за який тіло досягне поверхні Землі, скориставшись формулою

.

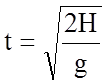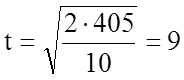Оскільки  м,  м/с², то  с.

Таким чином, треба знайти найбільше значення функції  на відрізку .

.

.

Точка  є кінцем відрізка , а точка  не належить цьому відрізку. Оскільки при  маємо , то найбільшу кінетичну енергію тіло матиме в момент зіткнення з поверхнею Землі

дж.

Задача 5.  Знайти асимптоти і побудувати графік функції .

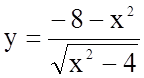Розв'язання.  1. Знайдемо область визначення функції

.

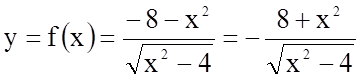Очевидно,  .

Визначимо поведінку функції, коли аргумент наближається до кінців інтервалів області визначення.

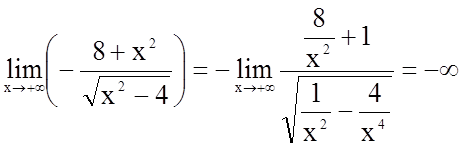; очевидно, також ;

;         .

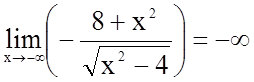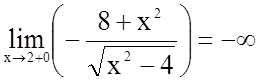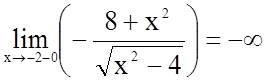Прямі   і  є вертикальними асимптотами графіка функції.

2. 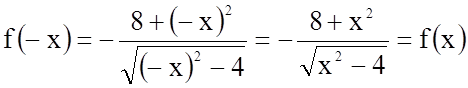 . Функція парна, її графік симетричний відносно осі .

3. Знайдемо похилі асимптоти

, де , .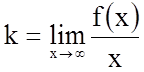

;

.

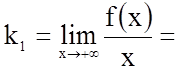
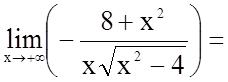
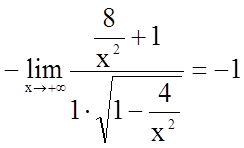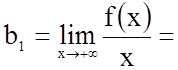
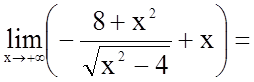
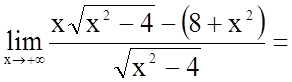
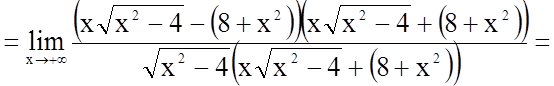
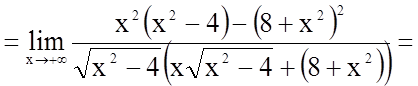
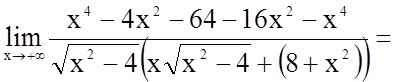
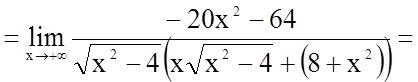
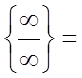
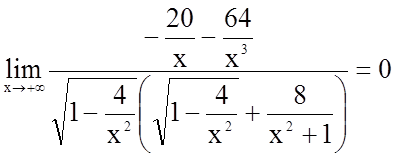Таким чином, пряма  є асимптотою графіка функції. Оскільки функція парна, то пряма  також є асимптотою її графіка.

4.

.

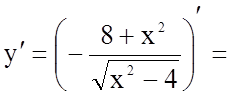
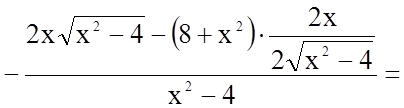
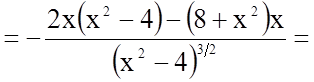
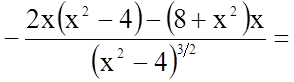
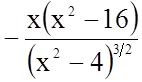а) Знайдемо точки, в яких похідна дорівнює нулю

;

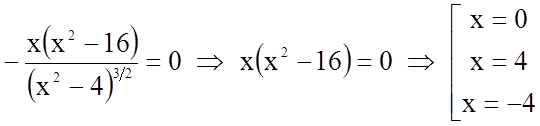 не належить до області визначення функції.

б) Очевидно, похідна існує в усіх точках області визначення.

Маємо дві критичні точки  і .

При  маємо , а при  маємо . Значить,  на інтервалі  функція зростає, а на інтервалі  – спадає. При  функція має максимум .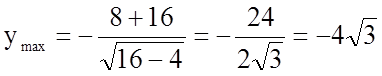

Оскільки функція парна, то  на інтервалі  вона зростає, а на інтервалі  – спадає і при  має максимум .

5. Виходячи з результатів дослідження, будуємо графік функції

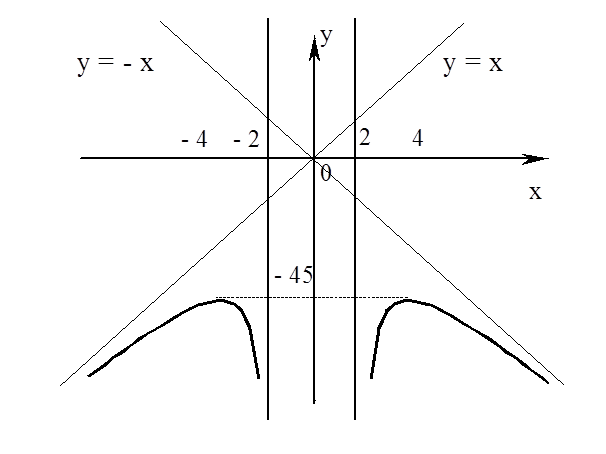Задача 6. Провести повне дослідження функції 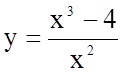 і побудувати її графік.

Розв'язання.  1. Знайдемо область визначення функції.

Очевидно, .

Визначимо поведінку функції, коли аргумент наближається до кінців інтервалів області визначення.

;      ;

;      .

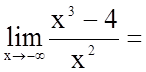
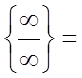
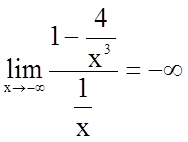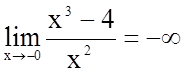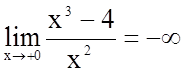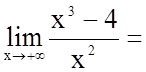
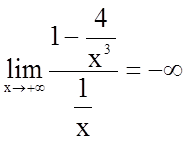Пряма  є асимптотою графіка функції.

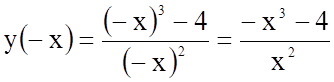
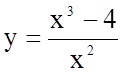2.      – функція загального вигляду.

3. Знайдемо похилі асимптоти

,  де  .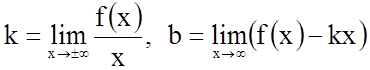

;

.

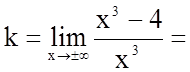
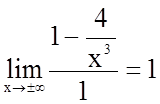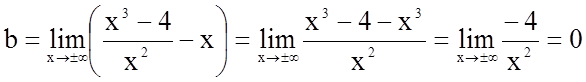Пряма  є асимптотою графіка функції.

4. .

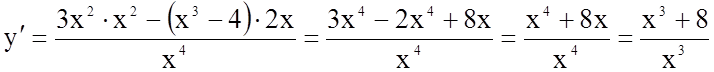а) Знайдемо точки, в яких .

.

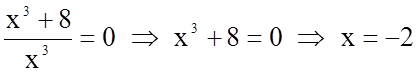б) Очевидно,  не існує в точці , яка не належить до області визначення функції.

Таким чином, функція має одну критичну точку .

5. .

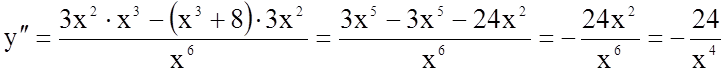а) Очевидно,  в жодній точці не дорівнює нулю.