б) ![]() не існує в точці
не існує в точці ![]() .
.
6. Зведемо дані дослідження в таблицю.
|
|
|
–2 |
|
0 |
|
|
|
+ |
0 |
– |
не існує |
+ |
|
|
– |
– |
– |
не існує |
– |
|
|
|
–3 |
|
не існує |
|
|
|
максимум |
|
асимптота |
|
7. Будуємо графік функції.
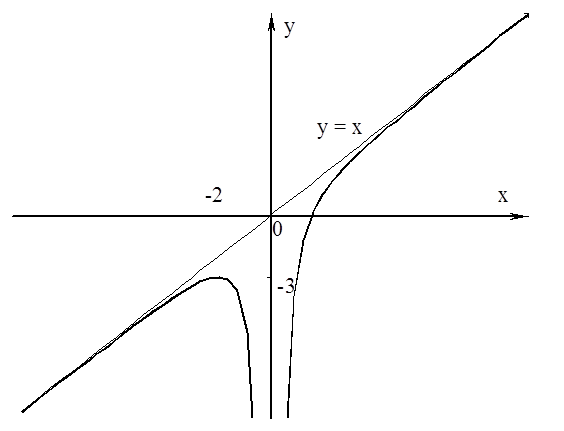
Задача 7.Провести повне дослідження функції 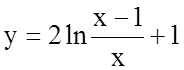 і
побудувати її графік.
і
побудувати її графік.
Розв'язання. 1. Знайдемо область визначення функції.
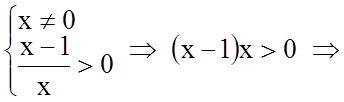
Таким чином, ![]() .
.
Визначимо поведінку функції, коли аргумент наближається до кінців інтервалів області визначення.
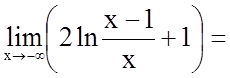
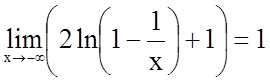 ;
;
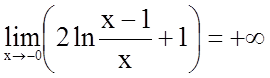 ;
;
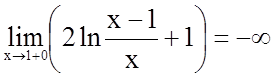 ;
; 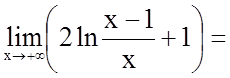
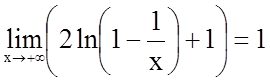 .
.
Бачимо, що пряма ![]() є
горизонтальною асимптотою, а прямі
є
горизонтальною асимптотою, а прямі ![]() та
та ![]() є вертикальними асимптотами.
є вертикальними асимптотами.
2. За формою області визначення робимо
висновок, що 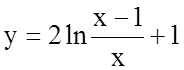 – функція загального вигляду.
– функція загального вигляду.
3. Знайдемо похилі асимптоти
![]() , де
, де 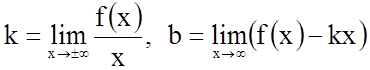 .
.
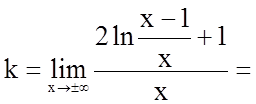
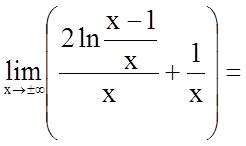
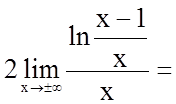
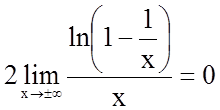 .
.
З цього виходить, що графік функції має лише
горизонтальну (з похилих) асимптоту, яку ми визначили раніше (![]() ).
).
4.
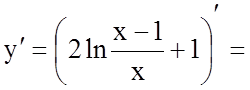
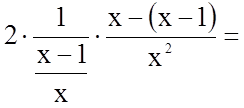
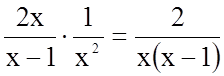 .
.
а) ![]() не дорівнює нулю в
жодній точці.
не дорівнює нулю в
жодній точці.
б) Очевидно, ![]() не
існує в точках
не
існує в точках ![]() і
і ![]() , які не
належать області визначення функції.
, які не
належать області визначення функції.
5.
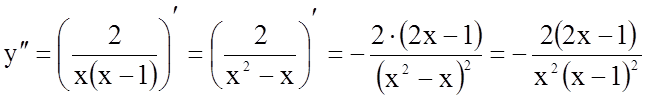 .
.
а) 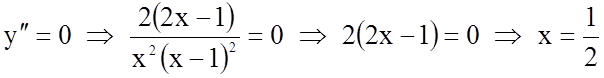 – не належить області
визначення функції.
– не належить області
визначення функції.
б) Очевидно, ![]() не
існує в точках
не
існує в точках ![]() і
і ![]() .
.
6. Зведемо одержані результати дослідження в таблицю.
|
|
|
0 |
1 |
|
|
|
+ |
не існує |
не існує |
+ |
|
|
– |
не існує |
не існує |
+ |
|
|
|
не існує |
не існує |
|
|
|
асимптота |
асимптота |
|
7.
Знайдемо точки перетину
графіка функції з віссю ![]() .
.
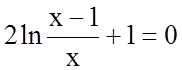 ;
; 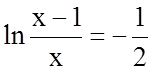 ;
; 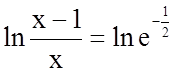 ;
; 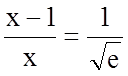 ;
;
![]() ;
; ![]() ;
; 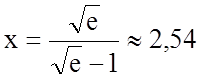 .
.
8. Будуємо графік функції.
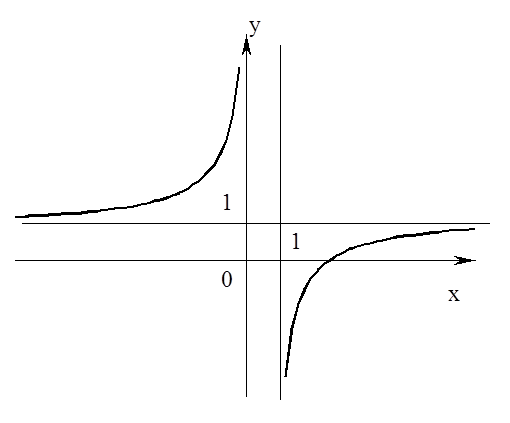
Задача 8. Провести повне дослідження функції ![]() і побудувати її графік.
і побудувати її графік.
Розв'язання. 1.Очевидно, областю визначення функції є множина всіх дійсних чисел, причому
якщо ![]() , то
, то ![]() ,
,
якщо ![]() , то
, то ![]() .
.
Вертикальних асимптот графік функції, очевидно, не має.
2. ![]() ;
; ![]() – функція загального вигляду.
– функція загального вигляду.
3. Знайдемо похилі асимптоти
![]() , де
, де 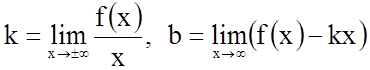 .
.
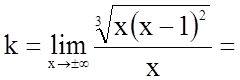
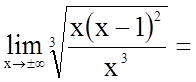
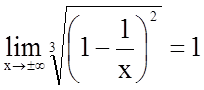 ;
;
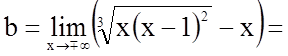
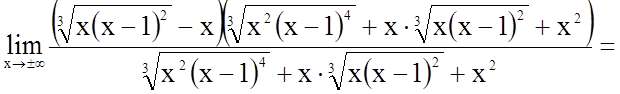
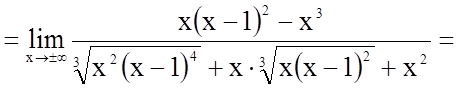
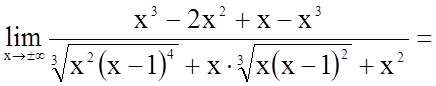
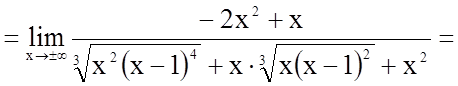
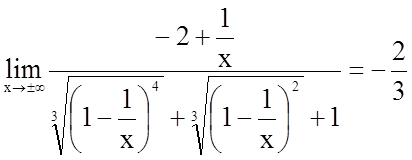 .
.
Таким чином, пряма 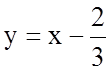 є
похилою асимптотою графіка функції.
є
похилою асимптотою графіка функції.
4. 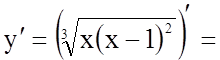
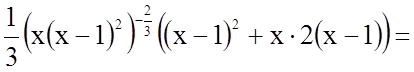
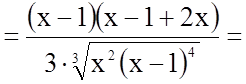
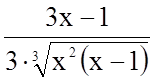 .
.
а) 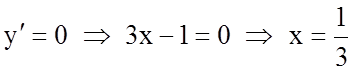 .
.
б) ![]() не існує, очевидно, при
не існує, очевидно, при
![]() , або
, або ![]() .
.
Функція має три критичні точки: 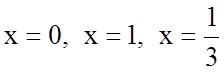 .
.
5.
![]()
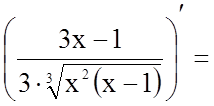
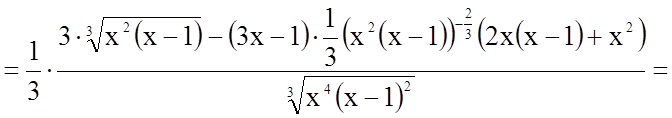
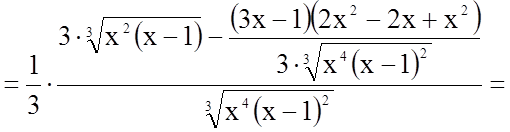
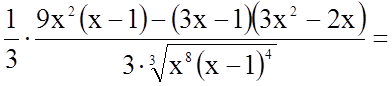
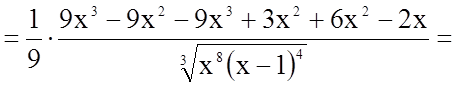
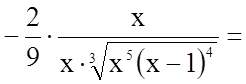
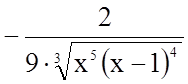 .
.
а) ![]() не дорівнює нулю в
жодній точці.
не дорівнює нулю в
жодній точці.
б) ![]() не існує, очевидно, при
не існує, очевидно, при
![]() та
та ![]() .
.
6. Зведемо одержані результати дослідження в таблицю.
|
|
|
0 |
|
|
|
1 |
|
|
|
+ |
не існує |
0 |
0 |
– |
не існує |
+ |
|
|
+ |
не існує |
– |
– |
– |
не існує |
– |
|
|
|
0 |
|
|
|
0 |
|
|
|
точка перег. |
|
максимум |
|
мінімум |
|
7. Будуємо графік функції.
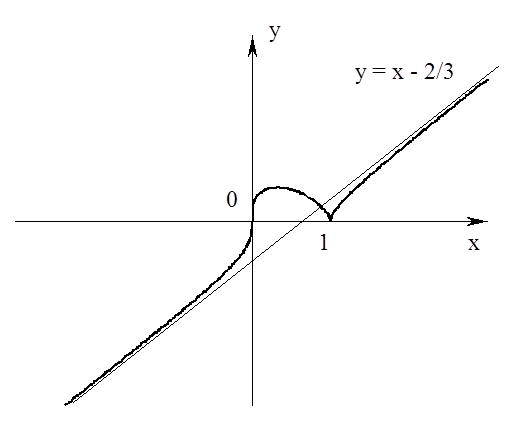
Задача 9. 1. Провести повне дослідження функції ![]() і побудувати її графік.
і побудувати її графік.
Розв'язання. 1. Знайдемо область визначення функції.
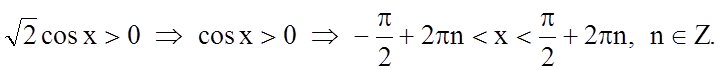
Таким чином, 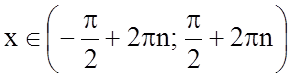 .
.
Очевидно, функція періодична з періодом ![]() .
.
Визначимо поведінку функції, коли аргумент наближається до кінців інтервалів області визначення.
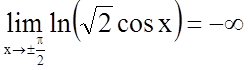 .
.
Звідси маємо, що прямі 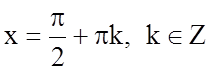 є
вертикальними асимптотами.
є
вертикальними асимптотами.
2.
![]() .
.
![]() – функція парна, її
графік симетричний відносно осі
– функція парна, її
графік симетричний відносно осі ![]() .
.
3.
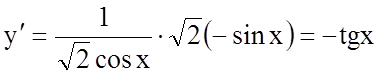 .
.
а) ![]() . Враховуючи область
визначення функції, маємо
. Враховуючи область
визначення функції, маємо ![]() .
.
б) ![]() не існує в точках
не існує в точках 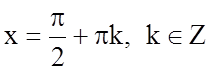 , які не належать області визначення
функції.
, які не належать області визначення
функції.
4.
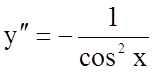 .
.
а) ![]() не дорівнює нулю в
жодній точці.
не дорівнює нулю в
жодній точці.
б) ![]() не існує в точках
не існує в точках 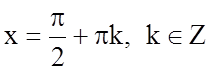 .
.
5.
Зведемо одержані дані в
таблицю (для відрізку 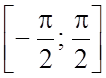 ).
).
![]()
|
|
|
|
0 |
|
|
|
|
не існує |
+ |
0 |
– |
не існує |
|
|
не існує |
– |
– |
– |
не існує |
|
|
не існує |
|
0 |
|
не існує |
|
верт. асимптота |
|
максимум |
|
верт. асимптота |
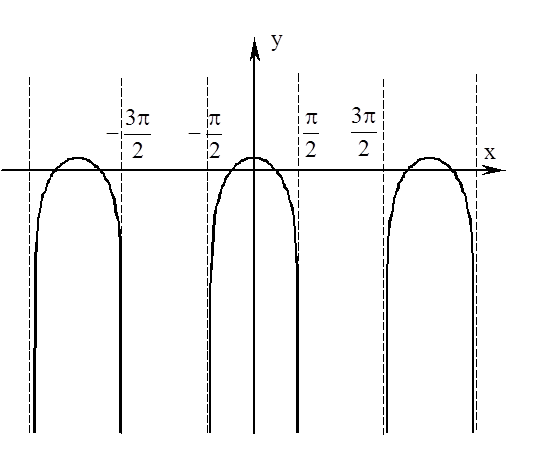
6. Будуємо графік функції, враховуючи її періодичність.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.