Промышленность \ Техника и технология переработки газа и конденсата

Техника и технология переработки газа и конденсата (Сборник с результатами исследований специалистов газовой промышленности, полученных в процессе работы), страница 18

2.  Парциальный мольный объем газа практически не зависит
от давления, хотя зависит от температуры.

3.  Газовый гидрат несжимаем, для него справедлива модель
"идеального" клатрата (это допущение введено только для просто­
ты изложения: совершенно аналогично можно использовать и мо­
дель регулярного клатрата).

4.  Неполярный газ слабо растворим в воде, а раствор газа

в воде можно рассматривать как идеальный (бесконечно разбавлен­ный). Для простоты изложения рассматривается однокомконентный

43


газ (соответствяяцее обобщение на многокомпонентную систему не содержит принципиальных трудностей).

При описании жидкой фазы (раствор газа в воде) воспользу­емся несимметричным способом нормировки, когда в качестве стан­дартного выбирается состояние бесконечно разбавленного раствора. Тогда химические потенциалы компонентов раствора запишутся

 ,  уН2;Нприх-о;

 £-4 при х-0. Здесь 4-х ,    х - мольные доли компонентов жидкой фазы, "Хно*   Хг ~ коэффициенты активности. Очевидно, можно принять

 интересует влияние вдменення внешнего давления на рав­новесие (при фиксированной температуре). Согласно принятым до­пущениям, зависимость стандартных химических потенциалов от дав­леная выражается следующим образом:

)

Ро= (U0325 МПа Тогда можно записать

Г()(

где     х - мольная доля газа в жидкой фазе (ниже при обсужде­нии равновесия   LH величина   х   рассматривается как функция внешнего давления);

Рр - давление, соответствующее трехфазному равновесию "газ - вода - гидрат" ( VLH ) при заданной температуре, поэтому Р 5» Р ; Уж - парциальный мольный объем воды в жидкой фазе;    \[ж - парциальный мольный объем газа в жидкой

Так как принято, что    V^ и    \/г   не зависят от  х и Р, то черту сверху можно опустить.

Химический потенциал вода в твердой (гидратной) фазе (см., например, / I / ) равен:


гле   М°'ТВ     - химический потенциал незаполненной клатратной

решетки при "нулевом" внешнем давлении (точнее при давлении на­сыщенного пара над гидратной решеткой);   Q  ,  02    - степени заполнения гидратяых полостей (малых и больших);     V. „  - пар-

цяальный мольный объем воды в гидрате (принимаем независящим от давления). Дяя гидрата кубической структуры I (например, гидра­та метана)     V,   = 1/23.    V2 » 3/23.

Поэтому прк давлениях Рр i P соответственно запишем

Отсвда

Введем для каддою типа клатратной полости свой химический потенциал включенного газа


-J»™(/О ■■■"«»&•

 V\

Здесь  JV\ri    (1/2)  - относится к "отандартной" степени за­полнения полости, равной Z/2. Индекс   I   характеризует тис полости. В рамках принятых допущений химические потенциалы вклю­ченного газа в полости зависят только от степени заполнения. Явная зависимость от давления отсутствует, так как парциальный мольный объем газа в клатрате с высокое степенью точности ра­вен нулю.

Учитывая, что   &,  и   8г ~ Функции давления Р, запишем химические потенщша» rasa з глатрате при давлениях Рр и Р:


Отсюда получаем

 Vql(p)

где   I = 1,2.

Очевидно, при внутреннем равновесии кяатратной фазы

Откуда следует взаимосвязь между  6., и   8г   :

сохраняющаяся при изменении внешнего давления Р.

При равновесии жидкой и твердой фаз имеет место равенство химических потенциалов

С учетом приведенных выше соотношений после некоторых пре­образований получим окончательную запись системы алгебраических уравнений, описывающих равновесие "растворенный в воде газ - га­зовый гидрат":


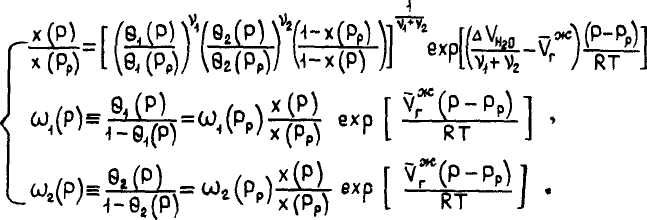
Здесь х (Рр).   94 (Рр'«   @г ^рр^ " заданные величины (опреде­ляемые из данных по трехфазному равновесию   VL,H )•

Система (I) трех уравнений с тремя неизвестными    X (Р). 8., №)»  84 CP) очень удойна для численного решения методом итераций.

Подход, развитый в / 3 /, можно рассматривать только как некоторое нулевое приближение прж решения системы (I).

Скачать файл