Техника и технология переработки газа и конденсата (Сборник с результатами исследований специалистов газовой промышленности, полученных в процессе работы), страница 10

Одаим из важных факторов, улучшающих качество управления химико-технологическими процессами и системами является возмож­ность уменьшения влияния измеряемых перекрестных возмущений, для целей практической реализации которой в настоящей работе ограни­чились передаточными функциями регуляторов-компенсаторов вида

по первому и второму каналу соответственно.

В отличии от классического подхода, благодаря характеру объекта управления, нами был разработан алгоритм синтеза циф­ровых регуляторов-компенсаторов (3) и (4) без использования па­раметрической оптимизации.

Алгоритм основан на использовании дискретных математических моделей каналов возмущений и управления объекта. При этом предва­рительно подвергнув к упрощению все непрерывные передаточные функции (I) - (2), а затем перейдя к их дискретизации при помощи

- преобразования с учетом экстраполятора нулевого порядка на входе каждого звена, после несложных выкладок,получили:

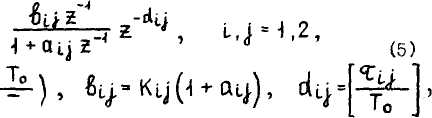
a буква "э' означает наличие экстраполятора нулевого порядка на входе каждого звена.

В соответствии,с теорией дискретная передаточная функция регулятора-компенсатора равна отношению передаточных функций объекта по каналам возмущения и управления, для реализации ко­торого должно выполняться следующее условие:

eta* <1ц , dy * dtz ,

что на практике почти невозможно.

Проведенный анализ показал, что идеальная компенсация возмущений, даже если она физически реализуема, вызывает труд­ности практического характера, связанные с наличием межтактовых

26

колебаний управляющей величины и больших ее отклонений при нейтрализации ступенчатых возмущений. Поэтому при практической реализации цифровой адаптивной системы управления обычно доби­ваются приближенной инвариантности системы по отношению к наи­более характерному виду контролируемых возмущений, что авторами и делалось в настоящей работе.

Из условий абсолютной инвариантности выходных величин от внешних возмущений и из выражений (I) - (5), в случае идеальной компенсации измеряемых внешних возмущений, для определения неиз-вестных параметров n_o,f\,f,, t«i,2  получим следующие две системы уравнений:

Г

4

h₀ - о«—О

Ьгг

 0 ,

из которых однозначно получим:

п₀ ⁼ Ьц/vn ,     ГЦ = пц По ,

В соответствии с теорией, для устойчивости выбранных циф­
ровых регуляторов-компенсаторов должно удовлетворяться необхо­
димое условие                .

|*/|   <U     L-4.2,

что выполняется для обоих каналов управления заведомо из-за ха­рактера объекта управления и свойства экспоненциальной функции.

Численный расчет, проведенный авторами в работе, подтвердил, что выбранный предлагаемым способом регулятор-компенсатор прак­тически компенсирует внешнее возмущение.

2?