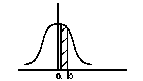
|
Плотность распределения – одна из форм закона распределения, которая существует для непрерывных СВ и обладает следующими свойствами:
1. f(x) ≥ 0 – функция плотности распределения не может принимать отрицательные значения.
2. Площадь, ограниченная кривой распределения и осью абсцисс равна 1.
18 Методика построения вероятностной модели
Для оптимизации процессов необходимо знать законы распределения и числовые характеристики всех действующих на процесс СВ. Поэтому при решении вероятностной задачи прежде всего необходимо определить законы распространения этих величин.
1 Построение модели начинается с определения разрядов и интервалов, в которые входит СВ. Далее строим вариационные рады, которые представляют собой 2 строки. В одной из которых приводится вариант, в другой – частот или частности.
2 Выполняется анализ вариационного ряда, его геометрического изображения (гистограммы), вычисляются параметры вариационного ряда и все это дает материал для предварительного выбора теоретического закона распределения.
3 Строим теоретический закон распределения. Записываем формулу нормального закона распределения.
4 Правильность сделанного выбора необходимо дополнительно проверить, т.е. решить задачу согласованности избранного закона теоретического распределения с имеющимся империческим (статистическим) распределением.
Степень близости эмпирического и теоретического распределений оценивается критериями согласия:
- критерий χ2;
- критерий Пирсона;
- критерий Смирнова и Калмагорова;
- критерий Романовского.
В том случае, если критерий согласия находиться в рамках допустимого, то наша гипотеза согласовывается с империческими данными.
Примеры и задачи оптимизации с вероятностными условиями:
Задача 1. Цехи ВРЗ имеют несколько одинаковых станков, которые время от времени выходят из строя. Предсказать время выхода из строя невозможно, т.к. он не зависим и не является СВ. Продолжительность устранения неисправностей также СВ, которая зависит от многих факторов.
Необходимо найти оптимальную численность наладчиков таким образом, чтобы полностью загрузить наладчиков с одной стороны, с другой – снизить продолжительность простоя станков.
Нормальный закон распределения.
Закон занимает особое положение и наиболее часто встречается на практике. Он является предельным законом, к которому приближаются все законы распространения и проявляются в тех случаях, когда СВ является результатом действия большого числа фактора..
Плотность вероятности этого закона заключается в виде:
Плотность распределения характеризуется 2-мя параметрами: мат. ожидание (m) и среднеквадратичное отклонение (σ).
Параметр σ характеризует форму кривой распределения:
– при увеличении σ кривая становится более плоской;
– при уменьшении – вытягивается вверх.
19 Методика определения расчетного значения фронта работ ВСУ
Одним из важнейших направлений по повышению эффективности технического обслуживания и ремонта грузовых вагонов является переход к вероятностным расчетным схемам.
Основополагающим фактором, определяющим расчет, является трудоемкость ремонта i-го типа вагона.
Предположим, что трудоемкость деповского ремонта вагонов описывается нормальным законом распределения
Где Hbi – трудоемкость ремонта вагона i-го типа;
- средняя трудоемкость ремонта вагона i-го типа;
- среднеквадратическое отклонение трудоемкости ремонта
вагона i-го типа.
Основными параметрами нормального закона распределения являются:
- математическое ожидание ();
- среднее квадратическое отклонение ()
Зная эти параметры, можно определить расчетное значение трудоемкости:
где tβi - среднее нормированное отклонение.
Будем считать, что годовая программа деповского ремонта должна быть реализована за год, - постоянная величина (Nдепi=const), а между продолжительностью нахождения вагона i-го типа в ремонте и трудоемкостью деповского ремонта существует линейная функциональная зависимость.
где a,b – эмпирические коэффициенты.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.