- стрелки не должны образовывать замкнутый цикл.
Для проверки опорного плана на оптимальность одной из вершин придается произвольное по величине число (потенциал).
Например, вершине I придадим потенциал 10. Тогда, перемещаясь только по стрелкам, вычислим потенциалы остальных вершин. Если стрелка выходит из вершины, то к потенциалу этой вершины прибавляется тариф. j= 4.5.6.7
Если же стрелка противоположна, то тариф вычитается из потенциала вершины, на кот. указывает стрелка.
Для вычисления оценки звена необходимо из большего
потенциала вычесть меньший, а полученную разность вычесть из тарифа 
где U- большее значение потенциала,
V- меньшее значение потенциала
Критерием оптимальности плана явл. условие 
для звеньев без стрелок.
Полученный план явл. оптимальным, т.к. оценки для звеньев без стрелок не отрицательны.
9 Методы решения сетевых транспортных задач
В настоящее время известно несколько методов (алгоритмов) решения сетевой транспортной задачи.
Общим для всех методом является решение задачи путем последовательных приближений.
Сначала создается задача на сети.
Картосхема сетевой задачи:
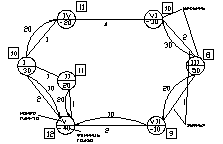
Пункты отправления и назначения изображаются на картосхеме в виде кружков, соединенных дугами. Дуги указывают дороги, которые связывают поставщиков и потребителей. Указываются также расстояния и единицы доставки груза. Положительные величины – запасы пунктов отправления, отрицательные – пункты потребления.
Имеем закрытую модель транспортной задачи на сети. Направление перемещения груза на сети будем указывать стрелкой.
Далее проводим оптимизацию плана. Условие оптимальности плана для сетевой задачи:
где rs – вершины, ограничивающие звено;
Crs – значение показателя оптимальности на звене rs;
хrs – корреспонденция на звене rs от вершины r к s.
Определяем показатели оптимальности для звеньев цепи.
Имея величины потенциалов для всех вершин, приступаем к проверке плана на оптимальность, используя приведенные выше уравнения.
Оптимальность полученного решения проверяется по определенным, различных для разных методов правилам. Если решение не оптимально, включаются поправки, после чего проверка на оптимальность повторяется.
Проверка выполняется рядом последовательных циклов (итераций).
Методы решения делятся на 2 группы:
- методы последовательного улучшения плана, которая в качестве исходного выбирает реальный вариант прикрепления. Исходное решение по данному методу является не оптимальным, т.е. имеющим общую сумму расходов на перевозку достаточно большой. Чтобы снизить ее, изменяется план в следующем методе расчета.
- основанных на сокращении невязок, предусматривает прикрепление в исходном варианте каждого получателя к наивыгоднейшему отправителю независимо от его ресурсов.
В общем случае получается вариант, формально дающий min целевой функции, но фактически нереальный, ввиду нехватки ресурсов у части отправителей.
Дальнейшие поправки направлены на постепенную разгрузку “перегруженных” отправителей с наименьшим возможным увеличением целевой функции. Первый достигнутый реальный вариант, в кот. выполняется условие будет оптимальным.
Правило изменения корреспонденции следующее. На звеньях, где направление корреспонденции совпадает с направлением корреспонденции, имеющей нарушение, величина хrs увеличивается, а на оставшихся – уменьшается. Величина улучшения определяется как
Улучшенную схему проверяем на оптимальность вновь. С этой целью необходимо определить потенциалы вершин. При этом нужно пересчитывать потенциалы для тех вершин, к которым вагоны поступают с других направлений, по сравнению с начальным планом.
Проверка условия оптимальности необходима для тех звеньев, у которых изменился потенциал хотя бы по одной из Верин.
Описанный выше процесс повторяется до тех пор, пока план не будет оптимальным.
Если при проверке на оптимальность окажется, что 
, то это указывает на существование
другого оптимального решения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.