Чтобы знать СВ прежде всего необходимо знать те значения, которые она может принимать. А также вероятность ее возникновения.
Среди СВ можно выделить два основных типа: дискретные и непрерывные.
Дискретные СВ могут принимать лишь последовательные цело-численные значения (число автопогрузчиков на складе, число поездов, проследовавших по гарантийному участку).
СВ, возможные значения которых непрерывно заполняют некоторый интервал числовой оси, относятся к непрерывным (число вызовов на телефонной станции за опред. время).
Совокупность значений СВ и соответствующих им вероятностей называется распределением СВ.
Параметры распределения – определенные постоянные величины, определяющие конкретное распределение.
Наиболее употребительными параметрами являются:
- среднее значение (m),
- дисперсия (Д)
- среднеквадратическое отклонение (σ=√Д).
Законом распределения СВ называется соотношение, устанавливающее связь между возможными значениями СВ и соответствующими им вероятностями.
Закон распределения дискретной СВ чаще всего имеет табличную форму изложения:
|
Xi Pi |
X1 P1 |
X2 P2 |
… … |
Xn Pn |
Для непрерывной СВ такой ряд не м. б. построен, т. к. она имеет бесчисленное множество значений. Поэтому закон распределения непрерывной СВ задается в виде функции распределения F(x). Эта функция служит формой выражения закона распределения и является универсальной характеристикой СВ для прерывных и непрерывных значений.
Величины называются зависимые друг от друга, если вероятность появления хотя-бы одной из них изменяется в зависимости появления или непоявления другой.
Если мы имеем дело с зависимыми СВ, то зная значения одной, можно указать закон распределения другой.
Пример СВ, связанных вероятностной зависимостью: СВ X – число отказов ЭВМ за год, СВ Y – стоимость затрат, связанных с поддержанием работоспособности ЭВМ. X и Y зависимы, т. к. при увеличении X, Y также увеличится.
Величины являются независимыми, если вероятность появления каждой из них не зависит от появления или непоявления прочих из них.
Две СВ называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая величина.
Пример независимых СВ: два стрелка стреляют каждый по своей мишени. СВ x1 – абсцисса точки попадания 1-го стрелка. СВ x2 – то же 2-го стрелка. Эти СВ независимы, т. к. причины, обуславливающие появление того или иного значения каждой из них различны.
Примеры СВ в процессах эксплуатации, ремонта и обслуживания ПС:
1) Трудоемкости ремонта вагонов и их узлов;
2) Затраты на техническое обслуживание и ремонт вагонов;
3) Значение параметров эксплуатационной надежности вагона (параметр потока отказов и наработка на отказ).
17 Вероятностные модели в расчетах
Одной из форм выражения закона распределения служит функция распределения.
Функцией распределения СВ Х называется функция F(x), выражающая вероятность того, что Х примет значение меньше, чем х, т.е.
F(x)=P(X<x)
Это универсальная характеристика СВ, которая может выражаться для непрерывной и прерывной СВ.
Эта функция называется интегральной функцией распределения или интегральным законом распределения и обладает следующими свойствами:
1. F(x) ≥ 0 (всегда неотрицательная функция).
2. т.к. вероятность не может принимать значения >1, то
0 ≤ F(x) ≤ 1.
3. Предельные значения функции распределения при
x=-∞ равно 0, а при х=+∞ равно 1.
Графическое обозначение F(x) для прерывной (а) и для непрерывной (б) СВ:
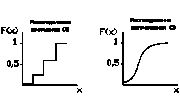
Производная от интегральной функции распределения, характеризующая плотность, с которой распространяется значение случайной переменной точке называется плотностью распространения или дифференциальной функцией распространения.
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.