Оптимальные решения и их свойства. Экономико-математическая модель оптимизационной задачи. Критерии оптимальности. Основные требования к локальному критерию оптимальности, страница 3

Если (имеется резерв мощности поставщиков) задача наз. открытой с превышением ресурсов.

Если , то эта задача открытого типа с превышением потребностей.

Экономико-математическая формулировка транспортной задачи состоит в следующем: имеется m отправителей и n получателей одного вида продукции. Заданы размеры ресурсов и потребностей по каждому отправителю и получателю. требуется составить такой план перевозок этой продукции, чтобы общая сумма затрат на ее транспортирования был минимальным.

Система ограничений:

 

                                                   (1)

Целевая функция

                                                             (2)

где xij – количество груза, перевозимого из пункта отправления i в пункт назначения j;

Cij – транспортные издержки перевозок единицы груза из пункта i в пункт j.

Требуется среди множества решений системы (1) найти такое неотрицательное решение, которое минимизирует функцию (2).                               

Транспортная задача в этой постановке решается на матрице, в строках которой показываются поставщики, в столбцах – получатели, в клетках (пересечение строк и столбцов) - корреспонденция между соответствующими поставщиками и потребителями.

Решаем задачу методом «северо-западного угла».

i=3, j=4

7 Методы решения матричных транспортных задач.

Существует до 10 методов решения транспортной задачи в матричной форме. Общим для всех методов является решение задачи путем последовательных приближений.

Сначала разрабатывается исходная схема прикрепления отправителей к получателям.

Затем по определенным различным для разных методов правилам проверяется оптимальность полученного решения. Если решение не оптимально, вносятся, после чего проверка на оптимальность повторяется.  Проверка выполняется рядом последовательных циклов (итераций)

Матричные методы решения делятся на 2 группы:

- методы последовательного улучшения плана, которая в качестве исходного выбирает реальный вариант прикрепления (*).  Исходное решение по данному методу является не оптимальным, т.е. имеющим общую сумму расходов на перевозку достаточно большой. Чтобы снизить ее, изменяется план в следующем методе расчета.

- основанных на сокращении невязок, предусматривает прикрепление в исходном варианте каждого получателя к наивыгоднейшему отправителю независимо от его ресурсов.

В общем случае получается вариант, формально дающий min целевой функции, но фактически нереальный, ввиду нехватки ресурсов у части отправителей.

Дальнейшие поправки направлены на постепенную разгрузку  “перегруженных” отправителей с наименьшим возможным увеличением целевой функции. Первый достигнутый реальный вариант, в кот. выполняется условие будет оптимальным.     

8 Транспортная задача в сетевой форме.

Транспортную задачу можно представить в сетевой форме. Для этого пункты отправления и назначения изображаются на картосхеме в виде кружков, соединенных дугами. Дуги указывают дороги, которые связывают поставщиков и потребителей. Указываются также расстояния и единицы доставки груза.

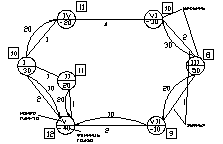
Положительные величины – запасы пунктов отправления, отрицательные – пункты потребления.

Имеем закрытую модель транспортной задачи на сети. Направление перемещения груза на сети будем указывать стрелкой.

При построении исходного плана необходимо соблюдать следующие условия:

-- все запасы полностью распределяются и удовлетворяется спрос потребителей;

- к каждой вершине сети подходит или выходит из нее хотя бы одна стрелка;

- общее число стрелок д.б. на единицу меньше числа вершин;