Оптимальные решения и их свойства. Экономико-математическая модель оптимизационной задачи. Критерии оптимальности. Основные требования к локальному критерию оптимальности, страница 23

Неизвестные коэффициенты модели (1) определяются из условия:

(2)

где n – число наблюдений, т.е длина временного ряда;

у_i – действительное значение показателя эксплуатационной надежности в i-й момент времени

t_i – год отстоящий от начального временного ряда

Дифференцируя выражение (2) мы получаем систему двух линейных уравнений, из которых определяем значения  а₀, а_1.

Расчет коэффициентов а₀, а₁ производится в предположении того, что ценность информации в начале периода наблюдения и в конце одинаково. В таком случае, в интервале времени от t₁ → t_n . Вес информации выступает как функция времени α_i =f(t).

Тогда с учетом α_i выражение (2) можно записать в следующем виде:

(3)

Тогда система уравнений для определения параметров а₀, а₁ запишется:

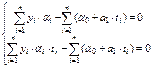(4)

Использование показателя «веса» информации, позволяет значительно повысить точность прогноза и ограничить влияние длительность ряда.

При прогнозировании с помощью рядов динамически можно подвергать анализу различные виды модели (линейные, степенная, показательная) выбор модели из трех возможных определяется с помощью остаточной дисперсии

S²_ост

Чем она меньше, тем лутшим образом модель описывает динамический ряд.

Для более полной характеристики соответствия модели временному ряду вычисляется коэффициент детерминации R² . Чем выше коэффициент детерминации тем точнее модель.

45, 46 Прогнозирование показателей эксплуатационной надежности вагонов по временным рядам. Сглаживание рядов.

В теории и практике прогнозирования встречается широкий спектр математических методов:

1) корреляционные функции;

2) экспоненциальное сглаживание;

3) вероятностно-статистические модели.

Происходит это в силу того, что основа всех процессов, происходящих на транспорте вероятностная. Рассмотрим один из наиболее распространенных методов прогнозирования по временным рядам. Важнейшим требованием к временным  рядам при построении модели прогнозирования является сопоставимость уровня показателей по методу сбора информации, усл. развития тенденции и т.д.

Особенность моделирования по временным рядам состоит в том, что рассм. уровни исследования величины выступают как случайные, т.е. динамический ряд реализует случайный процесс.

Для установки общей тенденции изм. исследуемого явления в течении изучаемого периода времени необходимо произвести сглаживание(выравнивание временного ряда). Эта необходимость обусловлена тем, что помимо влияния на уровне главных факторов, под воздействием которых и формируется тренд динамического ряда, на них действуют еще и случайные факторы.

С учетом сказанного модель прогнозируется получить с использованием линейной зависимости

(1)

Где   -коэффициенты, которые устанавливаются с использованием методов наименьших квадратов. Неизвест. коэффициенты модели (1) определяется из условия

Что сумма квадратов разности факт. и теоретич.

Где  n – число наблюдений. т. е. длина временного ряда

y_i – действит. значение покозателя  эксплуатационной надежности в i-тый момент     времени.

ti – год отстоящий от начального года временного ряда.  

Дифференцируя выражение(2), мы получаем сумму 2-ух линейных выражений, из кот.определяем   и     

Расчет коэффициентов a₀,a₁ и    производится в предположении того, что ценность информации вначале периода наблюдения и в конеце одинакова. В таком случае, в интервале времени от ti до tn вес информации выступает как функция времени , тогда с учетом     выражение (2) м. записать и следуещем виде

(4)

Тогда система уравнений для определения параметров   и     запишется

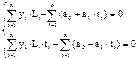(5)

Использование показателя веса информации позволяет значительно повысить точность прогноза и ограничить влияние длительности ряда. При прогнозировании с помощью рядов динамики можно подвергать анализу различные виды людей( линейная, степенная, и т. д. Выбор людей из 3-ех возможных определяется с помощью остаточных дисперсий, чем меньше величина остаточной дисперсии, тем наилучшим образом модель описывает динамический ряд.

Для более полной характеристики соотв. модели ряду вычисляют коэффициент детерминации. Чем выше коэф. детерминации, тем точнее модель.