Оптимальные решения и их свойства. Экономико-математическая модель оптимизационной задачи. Критерии оптимальности. Основные требования к локальному критерию оптимальности, страница 5

10 Определение оптимального варианта обеспечения грузового вагонного депо объектами ремонта. Математическая формулировка задачи.

Этапы решения задачи:

1 Определяется тип данной задачи (транспортная);

2 Выбирается метод решения (метод последовательных приближений);

3 Строится начальный вариант прикрепления пунктов отбора вагонов в ремонт к депо методами северо-западного угла, наименьшего значения показателя оптимальности и двойного предпочтения;

4 Проверяется условие оптимальности начального плана методом потенциалов;

5 При нарушении оптимальности плана производится его улучшение до тех пор пока не будет выполнено условие оптимальности.

Данная задача относится к транспортной задаче и имеет соответственно целевую функцию и ограничения.

Целевая функция

где Cij – затраты в стоимостном натуральном выражении на передачу одного вагона из пункта i и пункт j;

xij – количество вагонов, доставляемых из i в j;

m – число пунктов, на которых возможен отбор вагонов в ремонт;

n – число пунктов расположения депо.

Условие закрытой транспортной задачи:

где ai – количество вагонов, требующих ремонта в пункте i;

m – количество пунктов, на которых возможен отбор вагонов в ремонт;

bj – количество вагонов, требующих ремонта, равное производственной программе депо, расположенного в пункте j;

n – количество вагонных депо.

Условие открытой транспортной задачи:

Транспортную задачу можно решить в матричной и сетевой формах.

11 Способы составления начального плана задачи обеспечения депо объектами ремонта

Трудоемкость решения транспортных задач значительно сокращается, если первоначальное распределение будет ближе к оптимальному. Начальный план д.б. допустимый, т.е. удовлетворять ограничениям

Исходная схема и условие задачи:

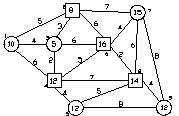
1-й способ: метод северо-западного угла(диагональный) не предусматривает использование стоимостных показателей.

Назначение корреспонденции x_ij  начинается с клетки, находящейся слева вверху, клетка (1,2). В эту клетку назначаем корреспонденцию, необходимую пункту 2, если это позволяет ресурс пункта 1. Столбец 2 исключаем из рассмотрения. Оставшийся ресурс пункта 1 (2 единицы) назначаем в клетку (1,4). Пункту4 не достает 10 единиц. Переходим к ресурсам пункта 3: все 5 единиц этого пункта назначаем в клетку (3,4). И в этом случае не удовлетворены потребности пункта 4. используем ресурс пункта 9. Из 8 единиц пункта 5 в пункт 4 направлены недостающие ему 5 единиц и т.д.

2-й способ: метод наименьшего значения показателя оптимальности дает решение более близкое к оптимальности, чем первый способ.