1)
![]() (1)
(1)
2)
Для точного
восстановления из последовательности отсчетов ![]() ,
нужно просуммировать все отсчеты с некоторым весом
,
нужно просуммировать все отсчеты с некоторым весом
![]() (2)
(2)
На
практике эту теорему часто формулируют иначе. Вместо шага дискретизации ![]() вводят понятие частота дискретизации
вводят понятие частота дискретизации
![]() .
. ![]() .
.
Тогда теорема Котельникова формулируется следующим образом:
Если
вещественный сигнал имеет конечную энергию и его двусторонний спектр ограничен ![]() , то возможна дискретизация сигнала
во времени и точное восстановление сигнала, если:
, то возможна дискретизация сигнала
во времени и точное восстановление сигнала, если:
1)
![]()
2)
![]()
![]()
Доказательство:
![]() , т.е.
, т.е. ![]() .
Если выбрать частоту дискретизации их этого условия, то тогда можно точно
восстановить сигнал.
.
Если выбрать частоту дискретизации их этого условия, то тогда можно точно
восстановить сигнал.
Докажем,
что ![]() нужно выбирать именно так.
нужно выбирать именно так.
Доказательство теоремы Котельникова выполним по Найквисту(на основе спектрально-инженерной трактовки этой теоремы).
Если
![]() , то
, то ![]()
![]() - финитный спектр исходного
непрерывного сигнала, превращенный в периодически повторяющийся спектр на оси
частот. Период повторения равен
- финитный спектр исходного
непрерывного сигнала, превращенный в периодически повторяющийся спектр на оси
частот. Период повторения равен ![]() .
.
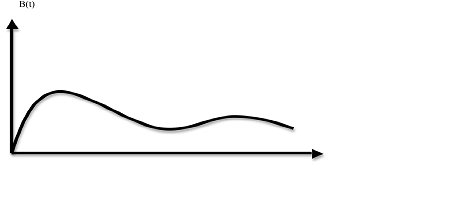
![]()
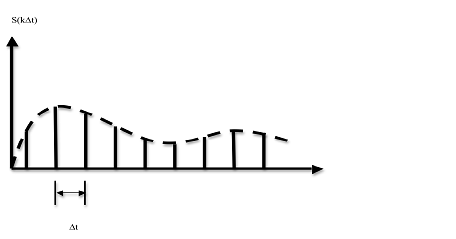
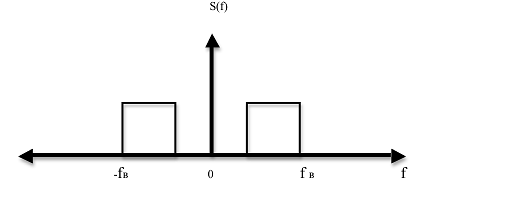
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.