Конспект лекций по теории электрической связи, первая часть, страница 33

Геометрическая модель сигналов. Сигнальные воздействия.

Все M сигналов могут быть представлены в виде совокупностей векторов.

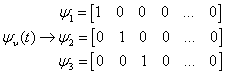
Все эти вектора попарно-ортогональны, то есть являются полной системой из  ортогональных осей координат (декартовой системой координат).

N-мерное пространство сигналов Евклида. Число сигналов будет одномерным пространством, :

 ….

(все сигнальные точки расположены на одной прямой)

 - то есть все  сигналов могут быть показаны в виде  векторов в 2-мерном пространстве.

…

…

 (концы векторов указаны точками)

…

…

(по четыре точки в каждом квадрате; то есть одна прямая задает 4 сигнала и лишь два линейно-независимых).

Метрические характеристики.

Длина вектора

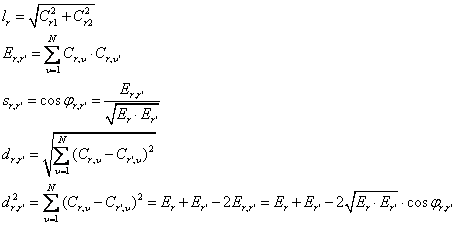
Процедура ортогонализации Грама-Шмидта.

Эта процедура является неотъемлемой частью теоремы о конечномерной модификации ОРФ.

Любой сигнал с конечной энергией может быть представлен с помощью N-мерного ОРФ, если задан не любой 1 или множество сигналов, а сигналов конечно и равно  ().

-базисные сигналы, базисные функции, несущие сигналы.

Конечное число ОРФ равно N мы получим только в том случае, если базисные сигналы будем формировать на основе процедуры ортогонализации, выполняемой над заданном множество сигналов.

Если же выбран произвольный ортогональный базис, то  может оказаться равным бесконечности, либо числом, значительно большим чем то, которое получилось из процедуры ортогонализации.