Конспект лекций по теории электрической связи, первая часть, страница 32

 (4)  ,

Возможность точного N-мерного представления обеспечивается благодаря тому, что в этом случае мы берем не любой ортонормированный базис (число которых велико), а специально подобранный базис для этих заданных  сигналов. Причем все базисы функции  определяются на основе того, что берем  заданных сигналов, а ортонормированный базис функции строим по заданным … сигналам на основе процедуры ортогонализации. Грама-Шмитда:

… (5)

В результате применения этой процедуры получаем, что верхний предел этой суммы  (6) . При этом  размерность равна числу сигналов, если все  заданных сигналов являются попарно ортогональны.

 если

N=1 если все  сигналов являются линейно-зависимыми. То есть любой сигнал с номером  может определяться как линейная сумма оставшихся сигналов.

-ранг матрицы Грама. Это матрица всех скалярных произведений:

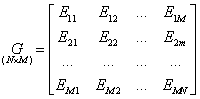
Элементы матрицы взаимной энергии при скалярном произведении:

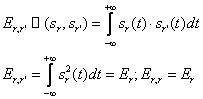
Ранг матрицы - минимальный размер подматрицы, определитель которой не ноль.

Если , то это значит, что в этой системе из сигналов есть линейно-зависимые сигналы.

-когда есть линейно-зависимый сигнал.

N=1-если все сигналы линейно-зависимые.

Когда есть все эти свойства – КМОРФ (конечномерный ОРФ).