Конспект лекций по теории электрической связи, первая часть, страница 19

              несущий

                       (carrier)

Каким будет преобразование Гильберта для модулированного сигнала?

Существует теорема Бедросяна:

Если спектр сигнала U(t) целиком лежит ниже, чем спектр несущего сигнала с(t), то преобразование Гильберта от их произведения:

͂с(t)

U(t) – НЧ сигнал через преобразователь Гильберта проходит без изменений. Преобразованию Гильберта подвергается только несущий сигнал (т. е. более высокочастотный)

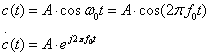
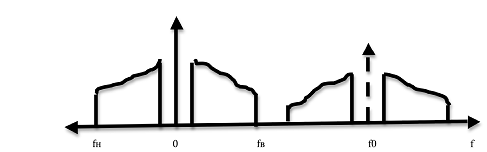
На практике модема строят таким образом, чтобы модулирующий сигнал и несущий были F-финитными.

В результате есть два преобразования из 3-х обязательных (Котельникова и Гильберта), для которых 1 обязательно, 2 желательно свойство F-финитности сигнала.

F-финитность - одна из проблем при реализации модема:

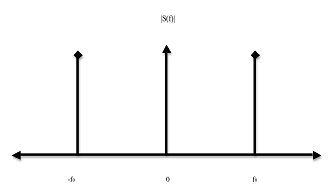
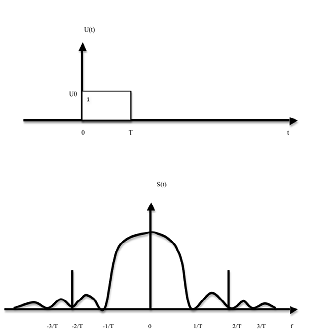
Спектр не является F-финитным!

Спектр наиболее распространенного сигнала не является F-финитным (теоретически бесконечен).

Вывод: ограничивают, другие подавляют (спектр делают F-финитным принудительно)

Что произойдет при этом?

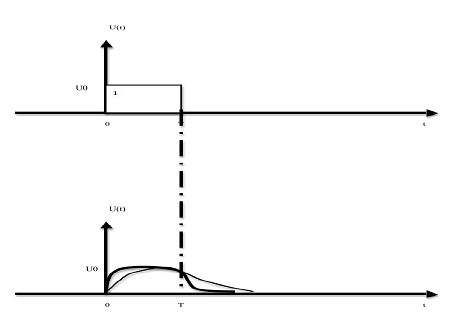
-форма прямоугольного импульса исказится

Основная проблема: сформировать модулированный сигнал с F-финитным спектром.

Есть два основных способа:

1)(самый радикальный) с самого начала применять модулирующие импульсы, имеющие F-финитные спектры- это модулирующие сигналы, форма спектра которых называются спектром Найквиста.

Искусственное ограничение верхней частоты спектра, тех импульсов, спектр которых теоретически бесконечен.

2) Пропускание исходного импульса через ФНЧ.