Конспект лекций по теории электрической связи, первая часть, страница 22

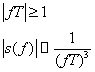
Дискретные преобразования Фурье.

Преобразования Фурье существует как для вещественных так и для комплексных сигналов Главное отличие: у вещественных сигналов  амплитудные спектры- есть четная функция частоты. Фазовый спектр – нечетная функция частоты. Для комплексного сигнала эти свойства не справедливы. Иногда эти спектры могут резко отличаться. Примером является аналитический сигнал, у которого мнимая часть сформирована по Гильберту.

С учетом этого, дискретное преобразование Фурье строится отдельно для вещественных и комплексных сигналов. fft=БПФ

       НПФ

Спектр будет непрерывным.

Переходим к дискретному преобразованию Фурье в два этапа.

1-ый этап:    Переходим к сигналу с дискретизацией по времени.

      

 где

-частота дискретизации

-частота Найквиста

Частота Найквиста-это частота среза фильтра нижних частот, который стоит до аналогового цифрового преобразователя и предназначена для ограничения верхней частоты спектра сигнала.

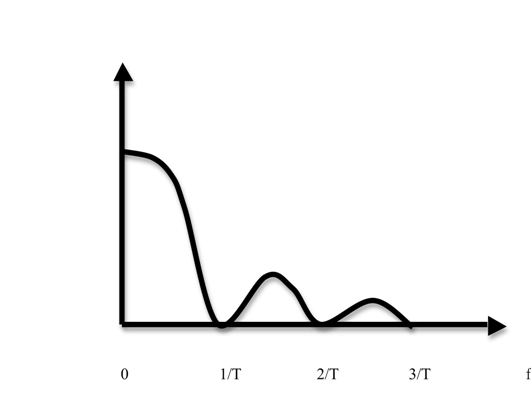
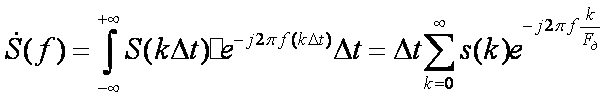
Реально сигнал задается на конечном отрезке времени.

,    

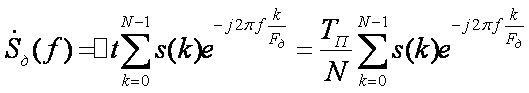
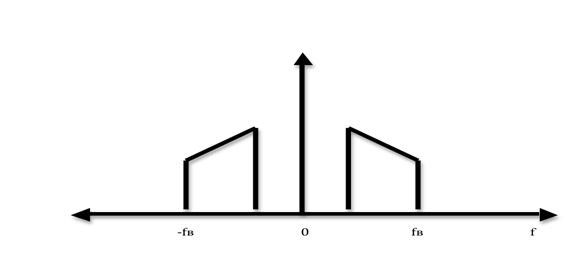
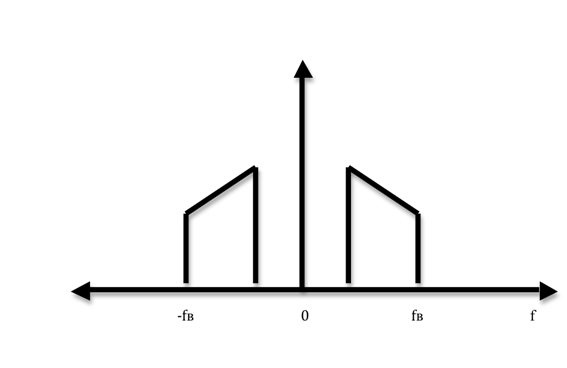
После дискретизации сигнала во времени -становится периодической функцией частоты, с периодом равным частоте дискретизации.