Конспект лекций по теории электрической связи, первая часть, страница 3

 УСЛОВИЯ ДИРИХЛЕ

1)  s(t) не должно иметь разрывов второго рода;

2)  s(t) может иметь разрывы первого рода, но число их должно быть конечным на отрезке времени, равном периоду сигнала.

Из условий Дирихле следует, что если они выполняются, то сигнал будет абсолютно интегрируемой функцией времени.

а)

б) s(t) есть интегрируемая по графику функция времени:

Смысл Е – энергия сигнала.

s(t) [B]          E[B²∙c]

Условий конечной энергии и конечной постоянной составляющей сами по себе недостаточно для того, чтобы существовал спектр периодического сигнала.

Условия Дирихле - более сильные и жесткие условия.

Если выполняются условия Дирихле, то для такого сигнала существует его разложение в ряд Фурье.

а) ;        (1)

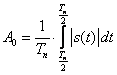
– гармонические колебания ( гармонические или спектральные составляющие сигнала)

A_k,  f_k ,  φ_{k –}   амплитуда, частота и начальная фаза каждого гармонического колебания.

, где k-число пер. гарм.  составл.

Вторая форма ряда Фурье имеет название квадратурной формы.

б)      (2)

в) самая компактная форма- комплексная форма ряда Фурье

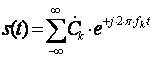       (3)

Во всех трех формах есть величина   ()- частота k-ой гармоники.

- частота первой гармоники; частота гармонического колебания, имеющего амплитуду    .

Первую гармонику часто называют основная гармоника.