Конспект лекций по теории электрической связи, первая часть, страница 7

 - шаг дискретизации

Значение сигнала в промежуточный момент времени не регистрируется и не обрабатывается.

 - время анализа сигнала,  - число отсчетов

Область применения дискретизации:

1)  возможность преобразования любых сообщений в цифровой формат. Для получения цифрового формата надо: а) дискретизация во времени б) квантование полученных значений

2)  частичное устранение избыточности передаваемого сообщения

3)  передача по одному каналу нескольких сообщений(уплотнение)

Основные проблемы, связанные с дискретизацией:

1)  как выбрать шаг дискретизации ? Чем меньше , тем точнее отображается передаваемый сигнал.  должен быть не слишком мал и достаточно большим, так как это позволяет снизить требования к объему оперативной памяти и требования к быстродействию.

Вывод: существует некоторая конкретная величина , которая должна позволять выполнять дискретизацию так, чтобы после нее можно было вновь точно восстановить непрерывное сообщение

2)  как на основе принятой последовательности отсчетов вновь абсолютно точно восстановить дискретизированное сообщение?

Перед нами два вопроса. Ответы на них дает теорема Котельникова.

Теорема отсчетов.

Два ограничения:

1)  энергия сигнала должна быть конечной

2)  Спектр сигнала(спектр Фурье) должен быть ограничен некоторой частотой

,

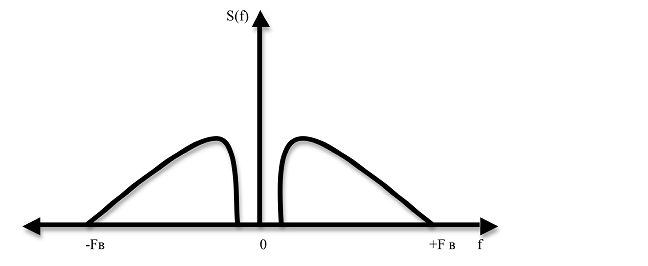
Теорема отсчетов:

Если исходный сигнал или сообщение  имеет конечную энергию и его частотный спектр ограничен верхней частотой , т.е.  при , то возможна дискретизация во времени и абсолютно точное восстановление, если шаг дискретизации выбрать из условия: