Конспект лекций по теории электрической связи, первая часть, страница 34

Наиболее известна процедура Грама-Шмитда:

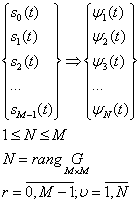
Либо , n-количество номеров базисных индексов.

 для  с номером

Если бы мы знали все базисные функции, то числитель формулы имел бы вид:

Первая сумма приведет части этой ОРФ для сигналов  (то есть это точное представление).

Вторая сумма в правой части -приближенное представление сигнала  с помощью суммы , где число членов суммы меньше того числа, которое нужно для точного представления сигналов с помощью меньшего числа коэффициентов ОРФ, то есть меньшего числа базисных функций.

Возьмем знаменатель формулы:

СКО - представление сигнала с (n-1) количеством.

 -  условие полноты базиса

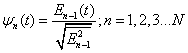
Рассмотрим частный случай:                  

                                                 

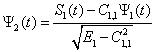                      и так далее

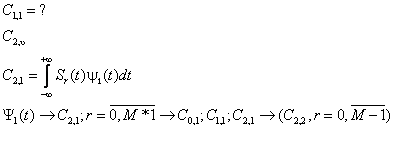
Рассматривается процедура ортогонализации Гр-Шм может дать М! возможных равноправных наборов базисных символов.

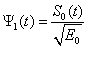      М

Для вычисления второй базисной – можно выбрать любой из оставшихся n-символов.

M(M-1)*(M-2)...  M!

Применение обратной процедуры КМОРФ для построения заданной системы  из М символов.