Конспект лекций по теории электрической связи, первая часть, страница 23

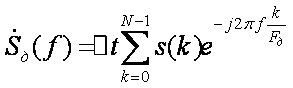
,  -известно в исходной задаче, поэтому ее опускают.

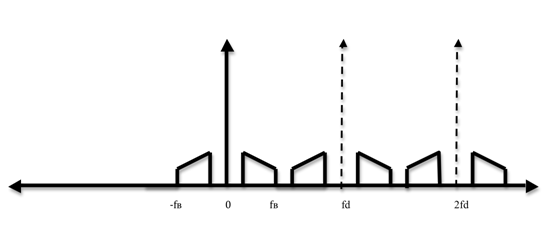
Получили спектр для сигнала в дискретном времени на непрерывной оси частот.

- сигнал считаем финитным, а для финитного сигнала его спектр можно представлять в виде интеграла Фурье.

-комплексный коэффициент ряда Фурье.

-частота первой гармоники

                          

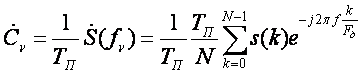
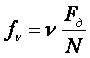
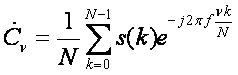;                 -Формула преобразования Фурье для вещественного сигнала.

 

Свойства дискретного преобразования Фурье

1)  Свойство цикличности дискретного преобразования Фурье, это то же самое, что свойство периодического повторения спектра сигнала после его дискретизации во времени. На непрерывной оси частот этот спектр повторяется с периодом равным частоте дискретизации.

2)  Если переходить к дискретному спектру, то Т будет равен частоте дискретизации. Вместо частоты  в расчетах участвует только номер гармоники . Тогда спектр при ДП будет повторяться с периодом равным N.