Геометрия космических полетов, страница 8

С помощью рис. 5.8С можно легко вычислить продолжительность теневого участка для любого положения Солнца относительно плоскости орбиты. В частности, на рис. 5.8D показан квадрантный сферический треугольник (quadrantal spherical triangle) (т.е. треугольник, одна сторона которого равна 90°) между полюсом орбиты, надиром и точкой, которая находится на горизонте Земли (на окружности, изображающей Землю). Пусть r –угловой радиус Земли, b_S – высота Солнца над плоскостью орбиты, а f/2 – половина угла, соответствующего теневому участку. Из зависимостей в квадрантном сферическом треугольнике (Приложение D) находим:

                                                         5.3а

Тогда продолжительность Т_Е теневого участка на круговой орбите:

T_E=P×(f/360°)                                                                                                 5.3b

где Р – период обращения космического аппарата на орбите.

Для нашего примера, r=60°, b_S выбран 25°, следовательно f=113°, а Т_Е=33 мин, как мы и ожидали. С помощью формул 5.3 можно определить продолжительность теневого участка для произвольного положения Солнца относительно плоскости орбиты для круговых орбит и приближенно оценить продолжительность теневого участка для орбит, близких к круговым. Соответствующим образом выбрав r, с помощью тех же формул можно определить время, на протяжении которого Солнце будет на определенном расстоянии над или под плоскостью орбиты. Приведенный пример показывает, как с помощью сферической геометрии, применяемой в анализе геометрии космических полетов, мы разобрались в поставленной задаче и вывели простые формулы для ее решения.

Пример 2. Определение направления на Солнце

Продолжив вычисления, которые мы начали в предыдущем примере, мы можем вывести зависимости для определения угла между произвольной гранью космического аппарата и направлением на Солнце при движении космического аппарата по орбите. Это позволит нам провести анализ теплового режима и оценить засветку Солнцем различных приборов на борту космического аппарата.

Предположим, что космический аппарат ориентирован на Землю: одна ось направлена в надир, а вторая ось перпендикулярна плоскости орбиты. Вычисления будем производить с помощью рис. 5.9, который аналогичен рис. 5.8. В этой системе координат, связанной с космическим аппаратом, нормаль к данной грани аппарата изображается точкой N на небесной сфере. Точка N остается неподвижной в связанной системе координат, также как направление в надир и нормаль к плоскости орбиты. Солнце совершает один оборот за виток по малому кругу радиусом. Этот радиус остается практически постоянным на протяжении всего витка. Буквой g обозначен угол между N и нормалью к плоскости орбиты. Угол DAz – это разница азимутов Солнца и точки N. При движении космического аппарата по орбите он равномерно изменяется от 0 до 360°. Если I – энергия солнечного света, падающего на поверхность, площадью А, К – солнечная постоянная в окрестности Земли = 1358 Вт/м², а b – угол между Солнцем и нормалью N к грани космического аппарата, то, в момент времени, когда Солнце освещает выбранную грань:

I=A×K×cosb 5.4

и по закону косинусов для сторон,

cosb=cosg×cos+sing×sin×cos(DAz)                                                       5.5

Максимальный и минимальный углы между Солнцем и N:

b_max=+g   и   b_min=|-g|                                                                          5.6

 и g постоянны для каждой выбранной орбиты и грани космического аппарата, в то время как DAz изменяется при движении по орбите.

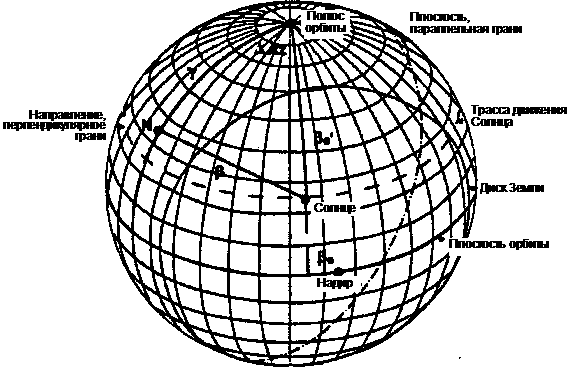
Рис. 5.9. Геометрические построения при вычислении угла между направлением на Солнце и нормалью к произвольной грани космического аппарата.

N представляет собой единичный вектор, или нормаль к выбранной грани космического аппарата. При движении космического аппарата по орбите видимое положение Солнца передвигается по пунктирной линии и длина дуги b между Солнцем и нормалью к грани изменяется по закону синуса.