Геометрия космических полетов, страница 15

Поскольку видимый путь движения космического аппарата представляет собой сложную геометрическую фигуру, то лучше всего его моделировать с помощью специальной программы. Рисунки в настоящей главе сделаны с помощью существующих коммерческих программ – Satellite Tool Kit [1990], Orbit View и Orbit Workbench [1991], Orbit II Plus [1991] и MicroGLOBE [1990]. Эти программы также могут работать и с эллиптическими орбитами и, совместно с приведенными в настоящей главе формулами, являются удобным инструментом для решения задач космической геометрии. К сожалению, моделирование не дает наглядности, не позволяет оно и быстро рассчитать геометрические зависимости для общего случая, что особо важно для начального этапа проектирования. Из-за указанных недостатков мы будем либо ограничивать рассматриваемые случаи, либо вычислять приближенно видимое движение космического аппарата, а не проводить точные вычисления. В конце концов, точные параметры отдельно взятого витка будут сильно зависеть от специфических геометрических условий. Точности приведенных ниже формул для космических аппаратов на круговых низких околоземных орбитах и геостационарных орбитах вполне достаточно для начальной стадии проектирования.

5.3.1.  Космические аппараты на низких круговых околоземных орбитах

Предположим, что космический аппарат, находящийся на низкой круговой околоземной орбите, проходит вблизи точки съемки или наземной станции. Предположим также, что его орбита настолько низка, что за время прохождения космического аппарата вблизи точки съемки или наземной станции можно пренебречь вращением Земли вокруг своей оси. Нам необходимо определить характеристики видимого движения космического аппарата для наблюдателя находящегося на наземной станции. В этом разделе мы будем пользоваться обозначениями, принятыми в разделе 5.2. Геометрические соотношения представлены на рис. 5.16. Малая окружность с центром в наземной станции показывает те положения подспутниковой точки, при которых высота космического аппарата над горизонтом e при наблюдении его с наземной станции превышает некоторую минимальную высоту e_min. Значение e_min будет зависеть от выполняемых космическим аппаратом задач (связь, дистанционное зондирование и т.д.). Для обеспечения связи космический аппарат должен быть не менее 5° над горизонтом, т.е. e_min=5°. Как указывалось при анализе рис. 5.14, радиус окружности зоны видимости сильно зависит от значения e_min. На рис. 5.16 высота орбиты принята равной 1000 км. Пунктирная линия с центром в наземной станции соответствует e_min=0° (т.е. действительному горизонту космического аппарата), а непрерывная линия – e_min=5°. На практике обычно выбирается какое-то одно значение e_min, которое и используется в расчетах. Однако вы должны помнить, что многие вычисляемые параметры очень сильно зависят от этого значения.

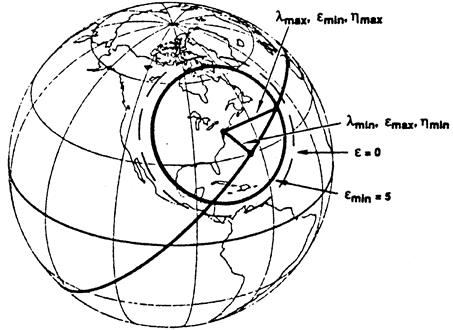
Рис. 5.16. Трасса космического аппарата относительно наблюдателя, находящегося на поверхности Земли.

Зная значение e_min мы можем определить максимальный центральный угол (maximum Earth central angle) l_max, максимальный надирный угол (maximum nadir angle) h_max, который измеряется между направлениями космический аппарат – надир и космический аппарат – наземная станция и максимальная дальность (maximum range) D_max, при которой космический аппарат еще будет виден с наземной станции. Эти параметры, которые вычисляются с помощью формул 5.25 – 5.27, равны:

sinh_max=cose_min×sinr 5.35

l_max=90°–e_min–h_max                                                                                          5.36

D_max=R_E×(sinl_max/sinh_max)                                                                               5.37

где

r – угловой радиус Земли, видимый с космического аппарата, т.е. sinr=R_E/(R_E+H).