Геометрия космических полетов, страница 5

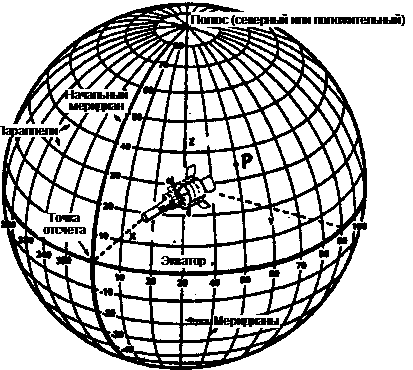
Рис. 5.5 Определение сферической системы координат на сфере единичного радиуса.

Азимут точки Р – 50°, высота над горизонтом – 35°, обычно записывают (50°, 35°).

Таблица 5.3

Названия координат в часто используемых сферических системах координат

*Также используется зенитное расстояние (zenith angle) = угол от точки, находящейся над головой наблюдателя, до данной точки = 90° минус высота над горизонтом; надирное расстояние (nadir angle) – угол между направлением на центр Земли и направлением на данную точку.

С помощью приведенных ниже уравнений можно преобразовать азимут Az и высоту над горизонтом El в соответствующие им координаты единичного вектора (x, y, z):

x=cos(Az)×cos(El)                                                                                            5.1a

y=sin(Az)×cos(El)                                                                                            5.1b

z=sin(El)                                                                                                          5.1c

Аналогично, для преобразования единичных векторов в соответствующие им сферические координаты используются следующие зависимости:

tg(Az)=y/x                                                                                                        5.2a

sin(El)=z                                                                                                          5.2b

Сферическая геометрия существенно отличается от геометрии на плоскости. Основополагающее отличие– в сферической геометрии нет параллельных линий. Это становится очевидным при рассмотрении двух меридианов, которые перпендикулярны экватору системы координат, но, тем не менее, пересекаются в полюсе. Аналогично, два любые больших круга, перпендикулярные третьему, пересекутся на расстоянии 90° от этого круга.

На рис. 5.6 представлен сферический треугольник, образованный двумя меридианами и экватором. Этот треугольник иллюстрирует еще одно основное свойство сферической геометрии. Оба угла вращения при экваторе являются прямыми углами. Поскольку угол у полюса больше нуля, то сумма углов в этом сферическом треугольнике больше 180°. Величина, на которую сумма превышает 180°, в нашем случае она равна углу у полюса, прямо пропорциональна площади сферического треугольника. Сумма углов сферического треугольника минус 180° называется сферическим избытком (spherical excess). Поскольку сферический избыток прямо пропорционален площади треугольника, то малые треугольники на сфере будут близки соответствующим им треугольникам на плоскости.

В планиметрии мы можем увеличивать или уменьшать размеры треугольников, сохраняя при этом отношение их сторон. В сферической геометрии это невозможно. Сферический треугольник однозначно описывается либо тремя его сторонами, либо тремя его углами. Дополнительная информация по сферической геометрии приведена в Приложении D. Там же приведены названия нескольких книг по сферической геометрии.

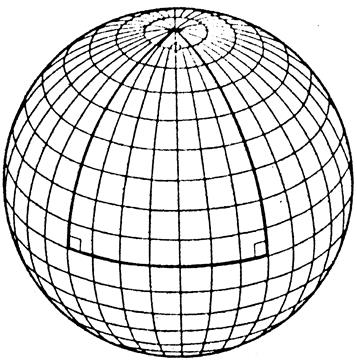
Рис. 5.6. Пример сферического треугольника с двумя прямыми углами.

Обратите внимание, что площадь треугольника пропорциональна сферическому избытку (spherical excess), т.е. величине, на которую сумма углов треугольника превышает 180°.