Геометрия космических полетов, страница 16

Мы будем называть малую окружность радиуса l_max с центром в цели эффективным горизонтом (effective horizon), который в нашем случае соответствует e_min=5°, в отличие от истинного или геометрического горизонта (true или geometrical horizon), для которого e_min=0°. Если подспутниковая точка лежит внутри эффективного горизонта вокруг цели или наземной станции, связь или наблюдение будет возможно. Длительность Т контакта и максимальная высота космического аппарата над горизонтом e_max будут зависеть от того, насколько близко трасса космического аппарата на данном витке проходит к наземной станции.

Как указано в Главе 6, плоскость орбиты космического аппарата, а следовательно и трассы, обычно определяется наклонением i и либо прямым восхождением W, либо долготой L_в.у. восходящего узла. Если не учитывать возмущения орбиты, то W, которое определяется относительно звезд, остается постоянным в инерциальном пространстве, в то время как поверхность Земли вращается. С другой стороны L_в.у определяется относительно поверхности Земли и поэтому за 1436 мин (период обращения Земли вокруг своей оси относительно звезд) возрастает на 360°. (Возмущения орбиты оказывают влияние на скорость вращения). Вследствие такого вращения орбиты относительно Земли, имеет смысл говорить о мгновенном восходящем узле (instantaneous ascending node) – L_в.у на момент проведения наблюдения или прохождения в зоне радиовидимости наземной станции. При проведении геометрических вычислений также целесообразно пользоваться мгновенным полюсом орбиты (instantaneous orbit pole), т.е. нормалью к плоскости орбиты на момент проведения наблюдения. Координаты мгновенного полюса определяются по формулам:

lat_п=90°–i                                                                                                        5.38

long_п=L_в.у.–90°                                                                                                5.39

Космический аппарат пройдет точно над точкой съемки или наземной станцией, находящейся на поверхности Земли, только в случае если

sin(long_НС–L_в.у.)=tglat_НС/tgi                                                                           5.40

Существуют два решения приведенного выше уравнения, которые соответствуют прохождению космического аппарата над наземной станцией на восходящей и на нисходящей частях орбиты. Для того, чтобы определить когда после пересечения экватора космический аппарат на круговой орбите проходит над наземной станцией, мы должны вычислить длину дуги m по мгновенной трассе от восходящего узла до наземной станции:

sinm=sinlat_НС/sini                                                                                           5.41

И в данном случае два решения соответствуют прохождению космического аппарата над наземной станцией на восходящей и нисходящей частях орбиты.

На рис. 5.16 минимальное расстояние между космическим аппаратом и наземной станцией определяется как минимальный центральный угол l_min между трассой и наземной станцией. Он будет равен 90° минус угловое расстояние, от наземной станции до мгновенного полюса орбиты, измеряемое из центра Земли, во время контакта. Если нам известны широта и долгота полюса орбиты и наземной станции (НС), то значение l_min вычисляется по формуле:

sinl_min=sinlat_п×sinlat_НС+coslat_п×coslat_НС×cos(Dlong)                                    5.42

где

Dlong – разница долгот НС и полюса орбиты.

В точке максимального приближения мы можем вычислить минимальный надирный угол h_min, максимальную высоту над горизонтом e_max и минимальную наклонную дальность D_min:

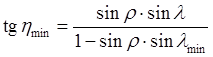                                                                               5.43

e_max=90°–l_min–h_min                                                                                          5.44

D_min=R_E×(sinl_min/sinh_min)                                                                                5.45

В точке максимального приближения космический аппарат будет двигаться перпендикулярно линии наземная станция – космический аппарат. Таким образом, максимальная угловая скорость  (maximum angular rate) движения космического аппарата при наблюдении с наземной станции будет равна: