Геометрия космических полетов, страница 11

Поток отраженного от Земли света и собственного излучения Земли несколько увеличит эффективное значение F. Это значение гораздо сложнее вычислить, чем F, уменьшенное за счет теневых участков, поскольку угловой размер Земли будет большим и интенсивность отраженного излучения не равномерна по поверхности Земли. Однако с достаточной точностью интенсивность излучения Земли можно принять равной:

-  475 Вт/м² для отраженного излучения (альбедо);

-  260 Вт/м² для собственного ИК излучения Земли (тепловое излучение).

5.2.  Земля, видимая из космоса

Наиболее распространенная задача в геометрии космических полетов – это определение относительной геометрии объектов на поверхности Земли, видимых с космоса. Один из примеров такой задачи – имея координаты цели на поверхности Земли, определить ее координаты в поле зрения прибора космического аппарата. Второй пример – найти координаты точка на поверхности Земли, которая соответствует заданному направлению в системе координат космического аппарата.

Для начала определим r – угловой радиус сферической Земли, видимый с космического аппарата и l₀ – угловой радиус области на поверхности Земли, которая видна с космического аппарата, измеряемый из центра Земли (см. рис. 5.10). Так как мы приняли, что Земля сферическая, то линия проведенная от космического аппарата до горизонта Земли, перпендикулярна радиусу Земли и, следовательно,

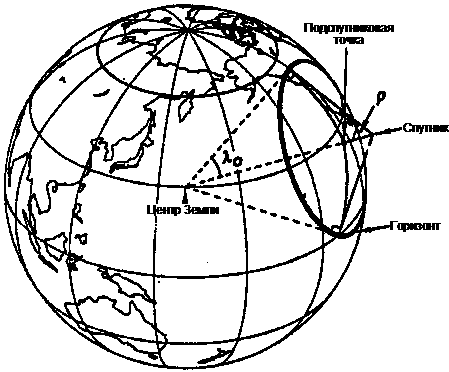
Рис. 5.10. Зависимости между геометрией, видимой из космоса, и из центра Земли.

См. также рис. 5.12.

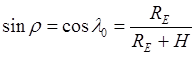                                                                                   5.15

и

r+l₀=90°                                                                                                         5.16

где

R_E – радиус Земли,

Н – высота орбиты космического аппарата.

Таким образом, Земля видна из космического аппарата как круг радиусом r и космический аппарат видит на поверхности Земли круглую область радиусом l₀. Расстояние D_max (см. рис. 5.12) до горизонта вычисляется по формуле:

D_max=[(R_E+H)²–]^1/2=R_E×tgl₀                                                                      5.17

Представление Земли в виде сферы дает точность достаточную для большинства задач. Однако для точных расчетов мы должны ввести поправку на несферичность. Учет несферичности Земли подробно описан у Liu [1978]. Несферичность Земли приводит к следующим двум отличиям Земли, видимой с космического аппарата, от идеального круга: во-первых, Земля кажется немного сплюснутой и, во-вторых, центр видимой сплюснутой Земли смещен относительно геометрического центра Земли. Во всех приведенных в этом разделе вычислениях мы используем сферические координаты как с центром на космическом аппарате, так и в центре Земли. Мы можем учитывать несферичность Земли и рельеф поверхности, просто задавая высоту точки съемки над или под поверхностью идеально сферической Земли. Для вычислений несферичность Земли и рельеф ее поверхности не имеет никакого значения, поэтому, результаты вычислений точны.

Нам необходимо найти зависимости между точкой съемки Т на поверхности Земли и космическим аппаратом, подспутниковая точка которого находится в точке SSP на поверхности Земли (см. рис. 5.11).Предположим, что широта подспутниковой точки d_S и ее долгота L_E известны. В зависимости от стоящей перед нами задачи нам может потребоваться: (1) по известным координатам цели на поверхности Земли определить ее положение в системе координат, связанной с космическим аппаратом, или (2) по известному направлению, заданному в системе координат, связанной с космическим аппаратом, определить точку пересечения этого направления с поверхностью Земли. В любом случае мы определяем относительное угловое положение точек SSP и Т, а затем преобразовываем полученные углы в координаты связанной с космическим аппаратом системы координат.