Геометрия космических полетов, страница 12

Зная координаты (L_S, d_S) подспутниковой точки, координаты (L_Т, d_Т) точки съемки и обозначив DL=|L_S–L_T|, мы можем определить азимут Az, измеряемый от направления на север по ходу часовой стрелки, и угловое расстояние l между подспутниковой точкой и целью (см. рис5.11). Формулы для вычислений:

cosl=sind_S×sind_T+cosd_S×cosd_T×cosDL    (l<180°)                                           5.18

cosAz=(sind_T–cosl×sind_S)/(sinl×cosd_S)                                                          5.19

где

Az<180°, если цель лежит восточнее подспутниковой точки и Az>180°, если цель лежит западнее подспутниковой точки.

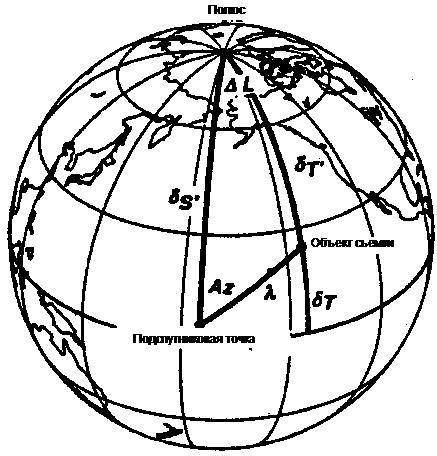
Рис. 5.11. Связь между точкой съемки и подспутниковой точкой на поверхности Земли.

С другой стороны, если известны координаты подспутниковой точки и положение (Az, l) цели относительно этой точки, то можно определить географические координаты точки цели:

cosd_T'=cosl×sind_S+sinl×cosd_S×cosAz    (d_T'<180°)                                          5.20

cosDL=(cosl–sind_S×sind_T)/(cosd_S×cosd_T)                                                        5.21

где

d_T'º90°–d_T,

Т лежит восточнее подспутниковой точки, если Az<180° и Т лежит западнее подспутниковой точки, если Az>180°.

Теперь преобразуем координаты на поверхности Земли в координаты связанной с космическим аппаратом системы координат. Вследствие симметричности азимут точки цели относительно направления на север не зависит от того, смотрим ли мы от космического аппарата или из центра Земли. Т.е.

Az_КА=Az_З=Az                                                                                                    5.22

Тогда, нам необходимо всего лишь найти зависимость между надирным расстоянием (nadir angle) h, измеряемым как угол между направлением в подспутниковую точку (в надир) и направлением на точку цели, центральным углом (central angle) l, измеряемым из центра Земли от подспутниковой точки до точки цели, и высотой космического аппарата над горизонтом (spacecraft elevation angle) e, измеряемой из точки цели между направлением на космический аппарат и местным горизонтом. На рис. 5.12 приведены указанные углы, а также расстояния, имеющие отношение к решаемой задаче. Прежде всего, находим угловой радиус Земли:

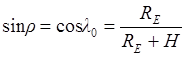                                                                                    5.23

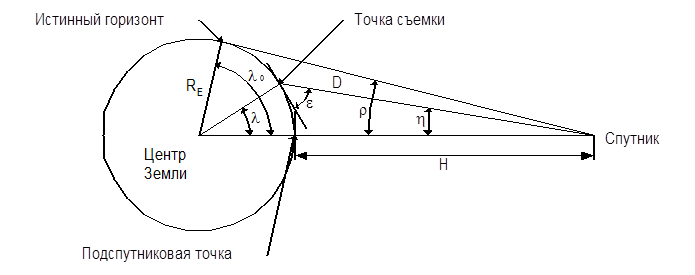
Рис. 5.12. Угловые зависимости между космическим аппаратом, целью и центром Земли.

Эта формула аналогична формуле 5.15. Далее, если известно l, находим h:

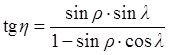                                                                                        5.24

Если известно h находим e:

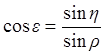                                                                                                     5.25а

Если известно e находим h:

sinh=cose×sinr                                                                                                5.25b

И, наконец, находим остальные углы и стороны:

h+l+e=90°                                                                                                      5.26

D=R_E×(sinl/sinh)                                                                                            5.27

Процесс перехода от связанной системы координат к геоцентрической системе координат представлен на рис. 5.13.

Вначале вычисляется угловой радиус Земли, r

5.23

По известным координатам подспутниковой точки (LS, dS), точки цели (LТ, dТ) и зная DL=|LS–LT| находим углы l, Az и h:

cosl=sindS×sindT+cosdS×cosdT×cosDL    (l<180°)                                        5.18

cosAz=(sindT–cosl×sindS)/( sinl×cosdS)                                                       5.19

5.24

По известным координатам подспутниковой точки и зная направление на цель, находим координаты на поверхности Земли:

5.25a

l=90°-h-e

cosdT'=cosl×sindS+sinl×cosdS×cosAz    (dT'<180°)                                       5.20

cosDL=(cosl–sindS×sindT)/(cosdS×cosdT)                                                      5.21