Геометрия космических полетов, страница 10

Если не выполняется ни одно из приведенных выше условий, то выбранная грань часть витка будет находиться в тени и часть витка освещаться Солнцем. В этом случае мы интегрируем мгновенную площадь проекции выбранной грани космического аппарата на плоскость, перпендикулярную направлению на Солнце, отнесенную к площади грани по мгновенному углу DAz, начиная и заканчивая интегрирование, когда угол b между нормалью к грани и направлением на Солнце равен 90°.

Деление на 2p дает среднее значение F за виток:

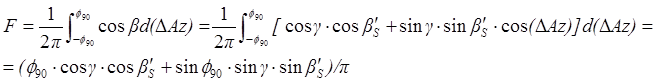 5.12с

(КА ориентирован в надир, периодическое затенение грани, бестеневая орбита)

где

f₉₀ выражается в радианах и

cosf₉₀=-1/(tgg×tg)                                                                                      5.13

Величина f₉₀ – это значение DAz при b=90°, т.е. при переходе Солнца через плоскость выбранной грани.

Рассмотрим предыдущий пример, для которого =65° и g=55°. В этом случае формула 5.12b применима и из формулы 5.13 находим f₉₀=109,1°. Это означает, что Солнце будет освещать выбранную грань, когда азимут Солнца находится в пределах 109,1° от азимута выбранной грани. Из уравнения 5.12а находим F=0,370. Это означает, что при отсутствии теневых участков средняя интенсивность потока солнечного света, падающего на выбранную грань космического аппарата, составляет 37,0% от максимальной интенсивности при постоянном падении солнечного света по нормали к грани. Если площадь грани составляет 0,5 м², тогда средняя интенсивность потока солнечного света, падающего на выбранную грань космического аппарата за виток на бестеневой орбите, равна 0,5´1358´0,370=251 Вт.

Космический аппарат, ориентированный в надир, вращается в инерциальном пространстве со скоростью один оборот за виток. Следовательно, приведенные выше зависимости можно использовать для космических аппаратов, вращающихся в инерциальном пространстве. При этом I_ср будет выражать среднюю интенсивность потока солнечного света за один период вращения космического аппарата. g в этом случае будет угол между осью вращения и нормалью к выбранной грани, а  – угол между осью вращения и направлением на Солнце.

На практике в приведенные формулы вводятся две поправки:

-  на теневых орбитах F снижается;

-  эффективное значение F увеличивается за счет отражения света от поверхности Земли и излучения Земли.

Как для космических аппаратов, неподвижных в инерциальном пространстве, так и для вращающихся космических аппаратов теневые участки просто уменьшают значение F на величину, пропорциональную продолжительности теневых участков:

F=F₀×(f/360°)                                                                                                 5.14

где

F₀ – значение F, определенное без учета теневого участка по формулам 5.11 или 5.12;

f – продолжительность теневого участка, определенная по формуле 5.3.

Для космического аппарата, ориентируемого относительно Земли, ситуация несколько сложнее, поскольку интенсивность падающего солнечного света зависит от положения Солнца относительно как Земли, так и грани космического аппарата, для которой вычисляется интенсивность. Пусть h – угол между  и надиром, а r – видимый угловой радиус Земли. Если нормаль к выбранной грани направлена достаточно близко к направлению в зенит (направление в зенит противоположно направлению в центр Земли) так что h–r³90°, тогда F=F₀ и значение F не уменьшится за счет теневых участков. При таком условии прохождение космического аппарата через теневые участки будут происходить, когда Солнце находится на обратной стороне интересующей нас грани. Теперь рассмотрим, что будет происходить, когда /g-/»90°. В этом случае солнечный свет попадает на выбранную грань только на небольшой части витка. Пусть f – продолжительность теневого участка, определенная по формуле 5.3, а f₉₀ – азимут, при котором Солнце переходит через плоскость выбранной грани. Если f³f₉₀, тогда в те моменты времени, когда Солнце может освещать выбранную грань, космический аппарат будет находиться в тени Земли. В этом случае F будет равно 0. Для промежуточных положений нормали к грани (между двумя рассмотренными крайними положениями) значение F будет в пределах от 0 до значения, которое мы получим на бестеневых орбитах. Численные значения могут быть вычислены по формулам 5.3 и 5.7.