Геометрия космических полетов, страница 18

Рис. 5.17. Движение космического аппарата, находящегося на орбите высотой 1000 км, при наблюдении с поверхности Земли.

Формулы приведены в тексте.

Полувысота h_накл и полуширина h_накл "восьмерки" при ненулевом наклонении i определяется следующим образом:

h_накл=±i                                                                                                            5.51

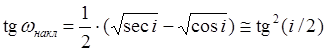                                                        5.52

где вторая формула – это приближение для малых i. Причиной этой "восьмерки" или аналеммы (analemma) является движение космического аппарата по орбите с наклонением, которая то отстает, то перегоняет равномерное вращение Земли вокруг своей оси.

Рис. 5.18. Видимое суточное движение космического аппарата, находящегося на геостационарной орбите.

Второй фактор, который приводит к неравномерному видимому движению, – это ненулевой эксцентриситет орбиты. Эксцентриситет орбиты е вызывает колебания в направлении восток–запад с амплитудой

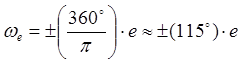                                                                         5.53

В общем случае видимое движение, вызванное ненулевыми наклонением и эксцентриситетом, накладываются друг на друга и в результате дают два возможных вида трассы космического аппарата на поверхности Земли. Если преобладает наклонение, то космический аппарат будет двигаться по "восьмерке". Если же преобладает эксцентриситет, то трасса будет овалом, как показано на рис. 5.18В.

Для космических аппаратов, находящихся на орбитах с высотами большими, чем у геостационарной орбиты наибольшее влияние оказывает вращение Земли вокруг своей оси, а не движение самого космического аппарата. Вследствие этого в данном случае удобнее всего рисовать движение космического аппарата относительно неподвижных звезд. В такой системе координат движение в неподвижной инерциальной системе координат может трактоваться тем же образом, что и видимое движение Луны или планет. Существует большое количество вводной литературы по небесной механике, в которых рассматривается данный вопрос. Например, Roy [1978], Green [1985] или Smart [1931].

5.4.  Составление сводок погрешностей географической привязки и наведения