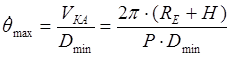Геометрия космических полетов, страница 17

                                                                           5.46

где

V_КА – скорость движения космического аппарата по орбите;

Р – орбитальный период.

И, наконец, удобно пользоваться суммарным азимутальным расстоянием Df (total azimuth range), которое проходит космической аппарат при наблюдении с наземной станции, суммарным временем Т нахождения в зоне радиовидимости (total time in view) и азимутом f_ц центра видимой дуги, где высота космического аппарата над горизонтом максимальна:

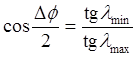                                                                                              5.47

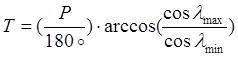                                                                          5.48

где arccos вычисляется в градусах.

Азимут f_ц связан с f_п – азимутом на проекцию полюса орбиты на поверхность Земли – следующей зависимостью

f_ц=180°–f_п                                                                                                      5.49

5.50

где f_п<180°, если полюс орбиты находится восточнее наземной станции и f_п>180°, если западнее.

В табл. 5.4 сведены все необходимые формулы и приведен пример расчета. Обратите внимание, что, как указано выше, Т особенно чувствительно к изменению e_min. Если, например, предположить, что наземная станция расположена на вершине горы и e_min=2°, то время нахождения в зоне радиовидимости возрастает на 15% до 14,27 мин. На рис. 5.17 приведено несколько трасс космического аппарата, находящегося на орбите с высотой 1000 км.

5.3.2.  Космический аппарат на геостационарной орбите и на более высоких орбитах

Один из важных особых случаев видимого движения космического аппарата является движение по геостационарной орбите, когда космический аппарат практически неподвижен относительно поверхности Земли. Высота геостационарной орбиты составляет 35786 км, а период – 1436 мин, что соответствует сидерическому периоду вращения Земли вокруг своей оси относительно неподвижных звезд. В Главе 6 рассмотрен долговременный уход космических аппаратов, находящихся на геостационарной орбите. В этой главе мы рассмотрим видимое суточное движение этих космических аппаратов для наблюдателя, находящегося на поверхности Земли.

Для удобства мы примем, что наблюдатель находится в центре Земли, и будем вычислять видимое движение космического аппарата для этого случая. Точное движение, видимое наблюдателем, находящимся на поверхности Земли, будет гораздо сложнее, поскольку в таком случае наблюдатель смещен от центра Земли. Но общий итог будет примерно тем же и вариации в видимом движении для каждой конкретной точки на поверхности можно вычислить отдельно.

Наклонение и эксцентриситет орбиты оказывают наибольшее влияние на видимое движение геостационарных космических аппаратов. Эти два фактора приводят к различным изменениям траектории видимого движения космического аппарата, что может вызвать замешательство, если источник возмущений точно не известен. Как видно из рис. 5.18А, трасса космического аппарата с ненулевым наклонением имеет вид цифры 8 с центром на экваторе.

Таблица 5.4

Вычисление параметров прохождения в зоне видимости наземной станции

Исходные данные для приведенного примера: полюс орбиты находится в точке с координатами lat_п=61,5°, long_п=100°; наземная станция находится на Гавайях в точке с координатами lat_НС=22°, long_НС=200°; минимальная высота космического аппарата над горизонтом e_min=5°.