12. ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ
12.1. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
Электростатическое поле является частным случаем электро-магнитного, оно создается в диэлектрике неподвижными в пространстве и неизменными во времени зарядами. Различают:
- линейный заряд: t= 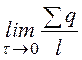 =
=![]() ;
;
- поверхностный заряд: s=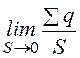 =
=![]() ;
;
- объемный заряд: r=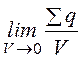 =
=![]() .
.
Основными величинами, характеризующими свойства этого
поля, являются его напряженность и потенциал. Если в электростатическое поле
поместить настолько малый пробный заряд, что он своим присутствием не
исказит его, то на него будет действовать сила ![]() , отношение
которой к величине заряда и даёт напряженность поля
, отношение
которой к величине заряда и даёт напряженность поля ![]() =
=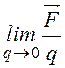 .
.
Размерность напряженности [E]
=![]() =
=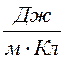 =
=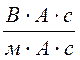 =
=![]() .
.
Электростатическое поле является потенциальным
или безвихревым во всем объеме. Записывается это следующим образом: rot![]() = 0,
= 0, 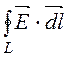 = 0.
= 0.
Для характеристики электростатического поля используется скалярный электрический потенциал j , удовлетворяющий условию
![]() = -gradj= -Ñ j .
(12.1)
= -gradj= -Ñ j .
(12.1)
Диэлектрические тела в электростатическом поле могут поляризоваться,
то есть может
происходить упорядоченное изменение расположения связанных зарядов под
действием сил поля. Степень поляризации характеризуется вектором
поляризации ![]() =
=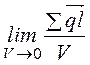 . Для большинства диэлектриков вектор
поляризации пропорционален напряженности поля:
. Для большинства диэлектриков вектор
поляризации пропорционален напряженности поля: ![]() = e0kэ
= e0kэ![]() , где
kэ- электрическая
восприимчивость.
, где
kэ- электрическая
восприимчивость.
В теории поля в расчет еще вводят вектор ![]() , который называется вектором
электрического смещения или вектором электрической индукции:
, который называется вектором
электрического смещения или вектором электрической индукции:
![]() = e0
= e0![]() +
+![]() = e0
= e0![]() + e0kэ
+ e0kэ ![]() = e0
= e0![]() (1 + kэ) = e0e
(1 + kэ) = e0e ![]() = eа
= eа![]() , где:
e= 1 + kэ- относительная
диэлектрическая проницаемость среды;
, где:
e= 1 + kэ- относительная
диэлектрическая проницаемость среды;
eа= e0e- абсолютная диэлектрическая проницаемость среды, в кото-рой создано поле.
Теорема Гаусса представляет собой основной закон электро-статического поля. Ее интегральная и дифференциальная формы записи:
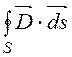 =
= ![]() , div
, div![]() = r.
= r.
Из теоремы Гаусса и соотношения (12.1) вытекают уравнения
Пуассона и Лапласа. Уравнение Пуассона: Ñ 2j = -![]() .
.
Частный вид уравнения Пуассона при r = 0 называется уравнением Лапласа:Ñ 2j = 0.
Решение уравнений Пуассона и Лапласа позволяет определить закон изменения потенциала по известному распределению заряда. При решении этих уравнений появляются постоянные интегрирования, которые определяются, исходя из граничных условий.
Граничные условия:
- граница диэлектрик-проводник: для всех точек диэлектрика, непосредственно примыкающих к поверхности проводника, равна нулю тангенциальная составляющая напряженности поля (Еt = 0), а вектор электрического смещения численно равен поверхностной плотности индуктированного заряда (D = s);
- граница диэлектрик-диэлектрик: для всех точек, являющихся общими для двух различных диэлектриков, равны по величине тангенциальные составляющие вектора напряженности (Е1t = Е2t) и нормальные составляющие вектора электрического смещения (D1n = D2n).
При расчёте электростатических
полей в однородных средах при наличии нескольких зарядов целесообразным
является применение принципа наложения. При этом найденные от отдельных зарядов
величины суммируются: скалярные – алгебраически (j =S±jq, U =S±Uq
и т.д.), векторные – векторно (![]() =S
=S ![]() ,
, ![]() =S
=S![]() ,
, ![]() =S
=S ![]() ).
).
При расчете полей, где имеется геометрически правильной формы граница раздела различных сред, применяется метод зеркальных изображений, сущность которого заключается в том, что влияние границы учитывается введением фиктивных зарядов, расположенных симметрично реальным относительно границы. Величина фиктивных зарядов определяется с помощью коэффициентов неполного отражения (коэффициентов фиктивных зарядов), которые в случае плоской границы диэлектрик-диэлектрик вычисляются по формулам
k1=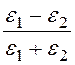 ; k2=
; k2=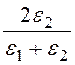 .
.
Электрические ёмкости рассчитываются для устройств, в которых электростатические поля не имеют зон с объёмно распределённым зарядом. Под ёмкостью C между двумя телами, на которых имеются равные и противоположные по знаку заряды, понимают абсолютную величину отношения заряда на одном из тел к напряжению между телами:
C = q/U.
энергия электростатического поля может быть определена по её объемной плотности wэ = ½DE = ½ee0·E2 = D2/(2ee0).
Энергия поля в объеме V Wэ =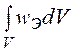 .
.
Силу, действующую со стороны поля на тело, изменение
положения которого влияет на энергию поля, можно определять через производную
от энергии: ![]() = -gradWэ. Сила в
некотором направлении х: Fх = -
= -gradWэ. Сила в
некотором направлении х: Fх = -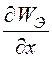 .
.
Для системы проводников с радиусами rk, расположенных вблизи проводящей поверхности, используют формулы Максвелла, основанные на применении метода зеркальных изображений.
I группа формул Максвелла: j 1 = a11t1 +a12t2 + a13t3 + … + a1ntn,
j 2 = a21t1 + a22t2 + a23t3 + … + a2ntn,
- - - - - - - - - - - - - - - - - - - - - - - - jn = an1t1 + an2t2 + an3t3 + … + anntn.
В этих уравнениях j k – потенциал проводников, t k– их заряды,
потенциальные коэффициенты aвычисляются по формулам
akk=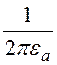
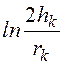 , akm =amk =
, akm =amk =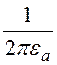
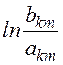 , где
hk – высота подвеса провода k, akm – расстояние между проводами k
и m, bkm – расстояние между проводом k
и изображением провода m.
, где
hk – высота подвеса провода k, akm – расстояние между проводами k
и m, bkm – расстояние между проводом k
и изображением провода m.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.