Электростатическое поле. Основные теоретические положения, страница 11

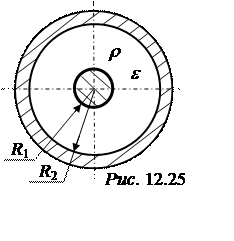
Задача 12.23. Симметричная сферическая система из двух металлических шаров находится в воздухе, удалена от земли и других тел на значительное расстояние (рис. 12.25). пространство между шарами заполнено диэлектриком с относи-тельной диэлектрической проницаемостью e=4, в котором распределен свободный заряд с равномерной плотностью  r= 5·10^-6 Кл/м³. Радиус внутреннего шара  R₁ = 20 cм, внутренний радиус сферической оболочки  R₂ = 40 cм. Рассчитать зависимости  E(R), j(R) для области  R₁ < R < R₂.

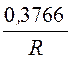Ответ.  E(R) = 47,08R – кВ/м,j(R) = -23,54R –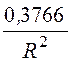+ 4,708 кВ, где  R[м].

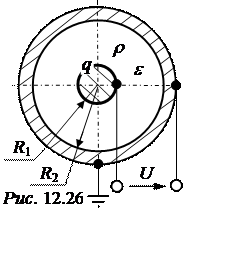
Задача 12.24. Объёмный заряд с равномерной объёмной плотностью  r= 10 ^-4 Кл/м³ распределён в диэлектрике (e= 4) между двумя шарами с размерами  R₁ = 4 cм,  R₂ = 10 cм (рис. 12.26). Шары подключены к источнику постоянного напряжения  U = 40 кВ.  Оболочка заземлена. Определить заряд q.

Ответ.  q= 1,096·10 ^-6 Кл.

12.4. МЕТОД ЗЕРКАЛЬНЫХ ИЗОБРАЖЕНИЙ

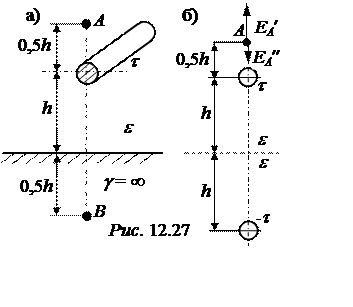
Задача 12.25. Проводник   с  зарядом  t = 10^-8 Кл/м  создаёт электростатическое поле вблизи металлической поверхности. Определить потенциал проводника, а также напряжённость и потенциал поля в точках  А и В  (рис. 12.27,а), если  r₀ = 2 см;  h = 4 м;  e = 1.

Решение

Электростатическое поле в точке В (внутри металла) отсутствует, поэтому  E_B = 0,  j_B = 0. Для расчёта поля в верхней полуплоскости рисунка применим метод зеркальных изображений. Коэффициент неполного отражения от идеального проводника равен -1. Расчетный рисунок принимает вид рис. 12.27,б, где два проводника с зарядами  t  и  -t  расположены в однородной среде с проницаемостью e. Далее применяем принцип наложения.

Напряжённость и потенциал от одной заряженной оси в однородной среде определяются в соответствии с формулами (12.5) и (12.10,а):

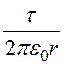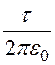E =,   j =ln.

Как видно из рис. 12.27,б, результирующая напряженность в точке А равна разности напряженностей от двух проводников. Таким образом, искомая напряженность в точке А:

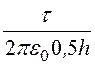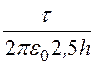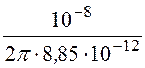
E_А = Е_А¢ – Е_А¢¢ =–== 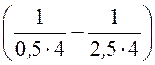71,93 В/м.

Потенциалы точки А и точки на поверхности проводника (потенциал проводника) определятся выражениями:

j_А = j_А¢ + j_А¢¢ =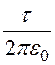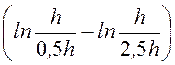=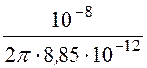ln5 = 290 В;

j =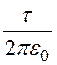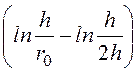=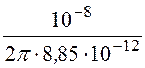ln= 1078 В.

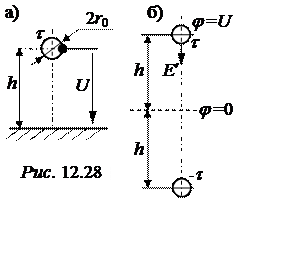Задача 12.26. Между проводником радиусом  r₀ = 1 см,  располо-женным в воздухе параллельно земле на высоте  h = 1 м,и землёй действует напряжение  U = 1000 В (рис. 12.28,а).

Определить ёмкость  С₀, энергию поля  W₀ и силу F₀, действующую на единицу длины проводника.

Решение

В соответствии с методом зеркальных изображений составляем расчётный рис. 12.28,б. Тогда потенциал проводника (см. задачу 12.25)

j = U =.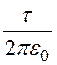

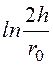Отсюда заряд провода

t =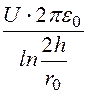==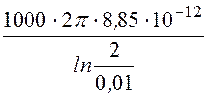 10,5·10 ^-9 Кл/м.

Ёмкость единицы длины линии   С₀ == 10,5·10 ^-12 Ф/м = 10,5 пФ/м.

Напряжённость поля, созданного зарядом -t  в месте расположения заряда  tв соответствии с (12.5)

Е¢ =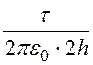==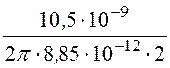 94,4 В/м.

Сила, с которой провод притягивается к земле

F₀ =t Е¢= 10,5·10 ^-9·94,4 = 0,991·10 ^-6 Н/м.

Энергия единицы длины линии

W₀ = ½С₀U ² = ½10,5·10 ^-12·10⁶ = 5,25·10 ^-6 Дж/м.

Задача 12.27. Между металлическим шаром ради-уса  r₀ = 10 см  и проводящей поверхностью (рис. 12.29) действует напряжение  U = 500 кВ.  Определить поверх-ностную плотность индуктированного заряда в точках А и В, если h = 4 м.

Ответы. q =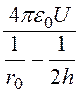;  Е_А =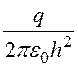;  s_А = D_А = e₀Е_А = 5,6·10 ^-8 Кл/м²;

s_B = D_B = e₀Е_B =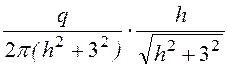= 2,87·10 ^-8 Кл/м².

Задача 12.28. В прямом углу, образованном двумя плоскостями проводящей поверхности в воздухе находится шар радиусом   R₀ = 1 см   с зарядом  q = 10^-10 Кл  (рис. 12.30,a). Определить потенциал шара по отношению к проводящей поверхности, ёмкость между шаром и проводящей средой, направление и величину силы, действующей на шар.

Решение

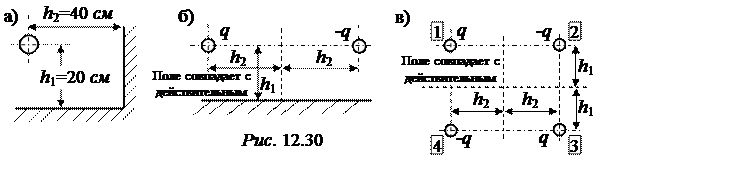В соответствии с методом зеркальных изображений после зеркального отражения относительно правой границы получим рис. 12.30,б. После вторичного отражения относительно нижней границы получим поле четырёх шаров в однородной среде (рис. 12.30,в). Применяя принцип наложения (см. задачи 12.2 и 12.3), получаем

j₁ =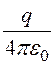(R₀^-1 – (2h₂)^-1 +()^-1 – (2h₁)^-1) = 87,55 В,

С == 1,14 пФ.