Электростатическое поле. Основные теоретические положения, страница 8

Суммарный заряд между электродами

Q=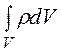==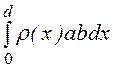 a·b·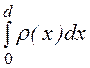= 25·100·=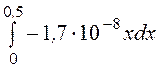

= -2500·1,7·10 ^-8·½·0,5² = -5,31·10 ^-6 Кл.

Примечание. Решение этой задачи с помощью системы MathCAD – см. задачу 12.42.

Задача 12.18. Решить задачу 12.10 с помощью уравнений Пуассона и Лапласа.

Решение

Общий вид уравнения   Ñ ²j = -  или  0. Совместим ось zцилиндрической системы координат с осью луча, тогда скалярный лапласиан запишется как    Ñ ²j =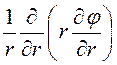++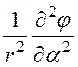    (см. табл. 11.1).

Но в данной задаче потенциал зависит только от одной координаты    r, то есть  = 0  и  = 0.  Таким образом, для двух различных областей получаем:

Ñ ²j ==

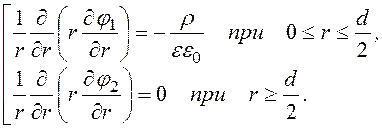
Двукратное интегрирование даёт:    j₁(r) = -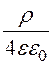r² + А₁ln(r) + А₂;

j₂(r) = А₃ln(r) + А₄.

Чтобы функция j₁(r) существовала при r = 0, слагаемое  А₁ln(r)  должно отсутствовать, то есть постоянная интегрирования  А₁ = 0.  Примем, что j₁ = 0  при   r = 0.   Тогда   А₂ = 0  и       j₁(r) = -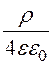r² = 1,412·10⁶·r².

Для напряженности    = -gradj = -––= -.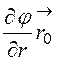

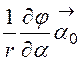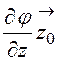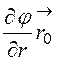Таким образом,  Е₁(r) = -=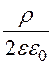r = -2,825·10⁶·r;   Е₂(r) = -= -.

Граничное условие –  D_1n = D_2n  или  eЕ₁ = Е₂  при   r = d/2:

e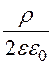= -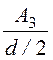;      А₃ = -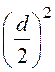= -= 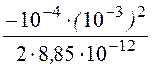5,65.

При   r = d/2    j₂(d/2) = j₁(d/2) = 1,412·10⁶·(10^-3)² = 1,41 В,  отсюда

А₄ = j₁(d/2) – А₃ln(d/2) = 1,41 – 5,65·ln(0,001) = 40,44.

Окончательно получаем

j(r) =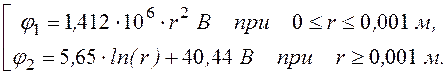

Е(r) =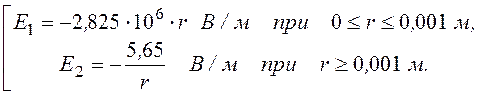

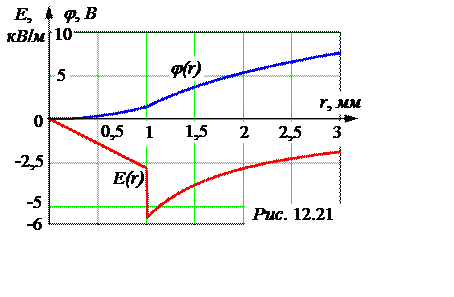
Построенные по этим формулам графики приведены на рис. 12.21.

Задача 12.19. В диэлектрике плоского конденсатора (ε₁ = 4) появилось длинное цилиндрическое воздушное включение диаметром   2а = 1 мм. Расстояние между пластинами  d= 20 мм  (рис. 12.22,а). Пробивные напряженности: для диэлектрика  Е_1проб = 120 кВ/см  и для воздуха  Е_2проб = 30 кВ/см.  Определить максимальные и рабочие напряжения, на которые может быть включен конденсатор, если:

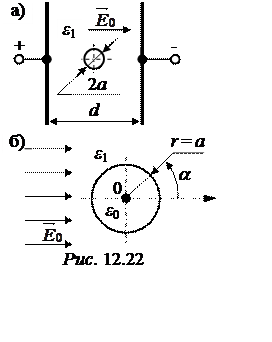а) в изоляции отсутствует воздушное включение;

б) в изоляции есть воздушное включение.

Принять в обоих случаях отношение пробивного напряжения к рабочему равным 3 (запас электрической прочности  n= 3).

Решение

а) Воздушное включение в изоляции отсутствует.

Поле конденсатора равномерное:    Е₀=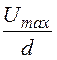= Е_1проб,   тогда

U_maх = dЕ_1проб =2∙120 = 240 кВ.

Рабочее напряжение      U=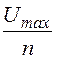== 80 кВ. б) В изоляции есть воздушное включение (рис. 12.22,б).

Ниже приведены полученные методом разделения переменных решения уравнения Лапласа для незаряженного цилиндра [3] (j(r, a)) и полученные дифференцированием этих решений формулы для напряженности электрического поля (Е(r, a)).

Для изоляции (область 1):      j ₁ = A₁ + (A₂r +)cos a,

E_1r = -= -(A₂ –)cos a,    E_1a = -= (A₂ +)sin a;

для внутренней воздушной области (область 2) аналогично: 

j ₂ = A₄ + (A₅r +)cos a,        E_2r = -(A₅ –)cos a,        E_2a = (A₅ +)sin a.

Заметим, что искажение равномерного поля цилиндром приводит к по-явлению слагаемых  в выражении для напряжённостей и слагаемых  – для потенциалов. Допуская 5% погрешности, можно заключить, что при         r> 20a  искажения картины распределения потенциала уже нет, а в напряжённости уже при  r> 5a  погрешность будет менее 4%. В нашей задаче а = 0,5 мм,  ½d= 10 мм,  соотношение между ними 20. Вывод: поле будет искажено только вблизи цилиндра. Поэтому при наличии цилиндрического неоднородного включения по-прежнему  Е₀= U/d.

Однако вблизи цилиндрического включения напряженность поля как в изоляции, так и в воздушном включении будет отличаться от Е₀, что может привести к пробою одной из сред, что недопустимо.

Постоянные интегрирования А₁÷А₆находим из граничных условий при   r= a,  а также исследованием решений при  r = 0  и  r = ¥.

Из условия непрерывности потенциала на границе цилиндра следует

А₁= А₄.                                               (*)

Первое граничное условие   E_1t= E_2t   приводит к равенству  E_1a= E_2a при   r= a:                                       А₂+= А₅ +.                                          (*)

Второе граничное условие  D_1n= D_2n  при  r= a  приводит к равенству e₁E_1r= e₂E_2r:                                   e₁(A₂ –) = e₂(A₅ –).                               (*)