Электростатическое поле. Основные теоретические положения, страница 4

Очевидно, что в данном случае потенциал  j  зависит только от одной координаты  R, то есть = 0 и = 0; вектор    направлен вдоль оси R, поэтому для его величины имеем:   E = -.   Отсюда

j = -=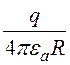+ А.                               (12.8)

Пусть потенциал наружного шара равен нулю –  j = 0  при  R = R₁. Тогда   А = -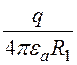.  Формула для потенциала     j =·.

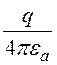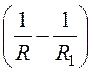Напряжение, приложенное к конденсатору,

U = j(R=r₁) – j(R=r₁) =·.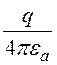

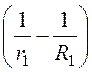Ёмкость однослойного конденсатора    С = q/U =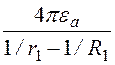.         (12.9)

Если конденсатор имеет несколько слоёв, то емкость каждого слоя –   С_k=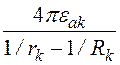, емкость всего конденсатора С =(S(С_k)^-1)^-1; напряжение на каж-дом слое –  U_k = q/С_k;  напряжённость поля в каждом слое –   E_k = q/(4pe_ak ·R²).

ЗАДАЧА 12.6. К шаровому конденсатору (рис. 12.6) приложено постоянное напряжение   U = 6000 В.   Геометрические размеры    r₁ = 5 см, r₁ = 10 см. Диэлектрическая проницаемость изоляции   e= 4.

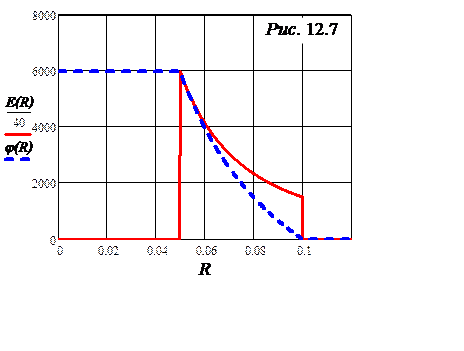Определить ёмкость конденсатора, построить графики E(r), j(R). Найти запасённую в диэлектри-ке энергию.

Решение

Воспользуемся формула-ми, полученными при решении задачи 12.5. Ёмкость конденса-тора

С ===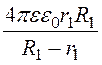 44,48 пФ.

Заряд конденсатора

q = СU = 26,69·10 ^-8 Кл.

Энергия заряженного конденсатора

W = ½СU ² = 0,8 мДж.

Напряжённость и потенциал в функции координаты  r [м]:

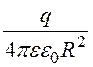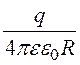E(r) == В/м,     j(R) =+ А.

Полагая, что j = 0  при  R = r₁,  получим j(R) =– 6000 В.

Графики  E(r) и j(R) представлены на рис. 12.7.

ЗАДАЧА 12.7. Сферический  конденсатор имеет два слоя изоляции (рис. 12.8,а):  R₁ = 5 см,  R₂ = 8 см, R₃ = 10 см,   R₄  = 10,5 см,  ε₁ = 6,  ε₂ = 2.  Конденсатор подключен к источнику постоянного напряжения  U = 36 кВ.  Определить емкость конденсатора, построить график Е(R). Найти  напряжение каждого слоя.

Решение

Емкость первого слоя:    С₁ =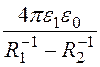= 88,97 пФ, а второго:     С₂ =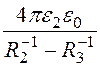= 88,97 пФ.

Емкость конденсатора, образованная последовательным соединением С₁ и С₂:

С =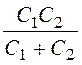= 44,48 пФ.

Заряд внутреннего шара:    q = CU = 1,6 Кл.

Напряженность поля в 1^ой области r₁≤r ≤ r₂,  где  r [см]

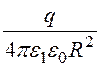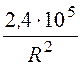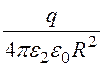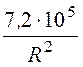E₁(r) == В/см, а во 2^ой области r₂≤r ≤ r₃       E₂(r) == В/см.

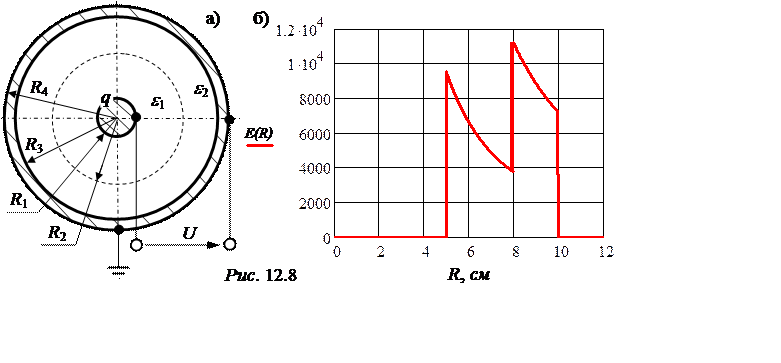График зависимости  Е(r) приведен на рис. 12.8,б.

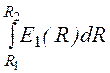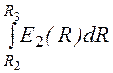Напряжение на первом слое изоляции:  U₁ == 18 кВ, а на втором:U₂ == 18 кВ.  

Проверка:  U₁ + U₂ = 18 + 18 = 36 кВ = U.

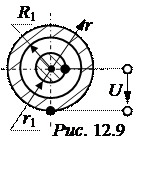
ЗАДАЧА 12.8. Вывести формулы для расчёта поля и ёмкости цилиндрического конденсатора, у которого внутренний и наружный радиусы диэлектрического слоя –

r₁ и R₁, причём длина  l >> R₁, диэлектрическая проницаемость изоляции –  e_a   (рис. 12.9).

Решение

Пусть внутренний цилиндр несёт на себе заряд  q.  На основании формулы (12.5) с учётом того, что   q = tl  находим электрическое смещение и напряжённость поля в диэлектрике      D = q/(2p ·r·l);     Е = q/(2pe_a·r·l).

Формулу для потенциала  j(r)  получим на основании соотношения (12.1). В цилиндрической системе координат   gradj   представляется как

gradj =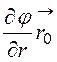++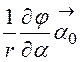  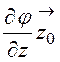  (см. табл. 11.1).

Очевидно, что потенциал  j  зависит только от одной координаты  r,  то есть = 0 и = 0; вектор    направлен вдоль оси  r, поэтому для его величины имеем:   E = -.  Отсюда

  j = -= -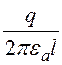lnr + А.                      (12.10)

Пусть потенциал наружной оболочки равен нулю –   j = 0   при   r = R₁. Тогда   А =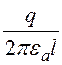lnR₁.   Формула для потенциала   j =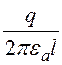ln.       (12.10,а)

Напряжение, приложенное к конденсатору,

U = j(r = r₁) – j(r = r₁) =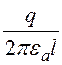ln.

Ёмкость однослойного конденсатора    С = q/U =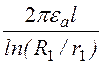.         (12.11)

Если конденсатор имеет несколько слоёв, то емкость каждого слоя –   С_k =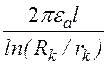,  емкость всего конденсатора –   С = (S(С_k)^-1)^-1;  напряжение на каждом слое – U_k= q/С_k; напряжённость поля в каждом слое – E_k = q/(2pe_ak·l·r).

ЗАДАЧА 12.9. К коаксиальному кабелю приложено постоянное напря-жение U = 6 кВ.  Длина кабеля  l= 20 м  (рис. 12.10).  Радиус жилы  r₁ = 0,5 см, радиусы оболочки  r₂ = 2 см,  r₃ = 2,4 см.  Относительная диэлектрическая проницаемость изоляции   ε = 4.

Пренебрегая краевым эффектом определить емкость кабеля, построить графики Е(r), j(r), найти запасенную в изоляции кабеля энергию.

Ответы: ёмкость кабеля по формуле (12.11)    С =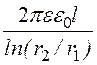= 3,21 нФ;