А2= -1,672 В/cм; А3 = 23·1,672·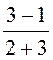
= 5,35 В·cм2; А5= -1,672·
= -1 В/cм.
Для точки А (область 2):
ERA = E2R 
= -А5cosqА = 1·cos60° = 0,5 В/cм,
EqA = А5sinqА = -1·sin60° = -0,866 В/cм,
EA =
= 1 В/cм; DA
= e2e0EA =
3·8,85·10 -14·1 = 26,55·10 -14 Кл/cм2.
Для точки В (область 1):
ERВ
= -(-1,672 –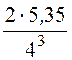
)·0,866
= 1,594 В/cм,
EqВ = (-1,672
+
)·0,5 = -0,7942 В/cм,
EВ =
= 1,781 В/cм; DВ =
e1e0EВ = 8,85·10
-14·1,781 = 15,76·10 -14 Кл/cм2.
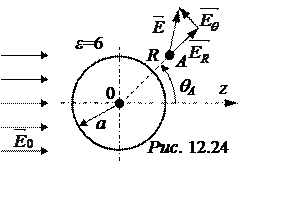
Задача 12.21. Проводящий заряжен-ный шар радиусом a = 5 мм помещен в равномерное электрическое поле с напряженностью Е0 = 4 кВ/см (рис. 12.24). Окружающая среда имеет относительную диэлектрическую проницаемость ε = 6. Найти значения напряжённости поля и вектора поляризации диэлектрика в точке А(7 мм; 40°; 0°), если заряд шара Q= 4∙10-9 Кл.
Решение
Решение произведём с помощью уравнения Лапласа в
сферической системе координат. При выбранном расположении осей (рис. 12.24)
потенциал не зависит от координаты α (
= 0),
поэтому данное поле будет описываться уравнением j =
+ (A2R
+
)cos q + A4, где
слагаемое определяется зарядом шара Q.
Для поля точечного заряда Q:
j =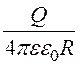
=, откуда A1 =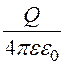
=
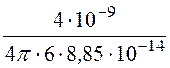= 600 В/cм.
Для определения остальных постоянных интегрирования используем напряжённость поля. Так как j зависит только от R и q, напряжённость имеет только две составляющие:
ER =
-
=
+ (-A2 +
)cos q,
Eq = -
= (A2 +
)sin q.
Из условий в бесконечности R® ¥получаем:
ER = -A2cos q = E0cos q, откуда A2 = -E0 = -4000 В/cм.
На границе раздела диэлектрик-проводящее тело нет
тангенциальной составляющей напряженности поля. Поэтому: Eq 
= 0,
откуда
A2 +
= 0 и A3 = -A2·а3 =
4000·53·10-3 = 500 В·cм2.
Таким образом: ER =
+ (4000 +
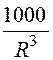)cos q, Eq
= (-4000 +
)sin q.
В точке А(0,7; 40°; 0°) ЕR = 4735 В/см, Еθ = -2596 В/см,
Е =
=
= 5400 В/см.
Определим вектор поляризации из соотношений 
= ee0
= e0+
.
Р = e0(e– 1)Е = 8,85·10 -14·(6 – 1)·5400 = 2,39·10 -9 Кл/см2.
Задача 12.22. Решить задачу 12.12 с помощью уравнений Пуассона и Лапласа.
Решение
В силу центральной симметрии устройства характеристики
поля зависят только от одной координаты – R, то есть = 0 и 
= 0. С
учётом этого уравнение в сферической системе координат (см. табл. 11.1) для
потенциала в зонах, занятых диэлектриком, принимает вид:
Ñ 2j =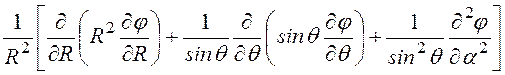
=
=
=
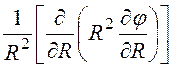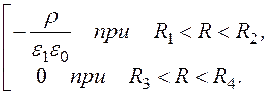
В результате двукратного интегрирования получаем:
j 1(R) = -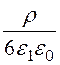
R2 –
+
А2; j 2(R) = –
+ А4.
Этих уравнений недостаточно для определения постоянных интегрирования А1÷А4, поэтому используем ещё напряженность поля:
= -grad j = -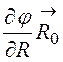
–
–
=
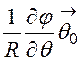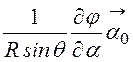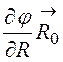-, откуда
Е1(R) = –
=
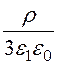R
–
; Е2(r) = –
= –
.
Для нахождения постоянных интегрирования на основании
граничных условий для границы диэлектрик-проводник (D
= s, jM1 = const) составим систему уравнений.
Учтём, что векторы 
и направлены по радиальным линиям и, следовательно,
имеют только нормальную составляющую. Примем, что за счет явления
электростатической индукции на внутренней стороне металлической прослойки появится
заряд -qпр, а
на внешней – +qпр.
При R = R1 j 1(R1) = U, при R = R4 j 2(R4) = 0, при R = R2 j 1(R2) = jпрослойки; при R = R3 j 2(R3) = jпрослойки;
или j 1(R2) = j 2(R3);
D1(R2)
= -s (R2) = -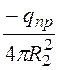
=
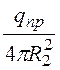, Е1(R2) =
=
;
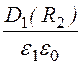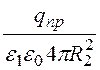D2(R3)
= s (R3) =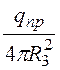
, Е2(R3) =
;
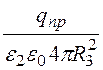или R22e1Е1(R2) = R32e2Е2(R3).
Следовательно, получается система уравнений:
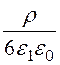-R12 –
+ А2 =
U, e1·R22·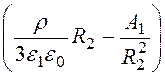
= e2·R32·
,
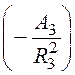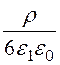-R22 –
+ А2 = -
+ А4, -
+ А4 = 0.
Подставляя в эти уравнения числовые значения и решая систему, получаем: А1 = 3,414; А2 = 1436; А3 = -94,87; А4 = -1897.
Записываем окончательные формулы потенциала и напряженности поля, по которым строим требуемые графики (рис. 12.14):
j(R) =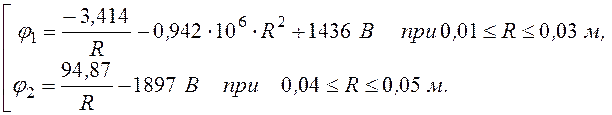
Е(R) =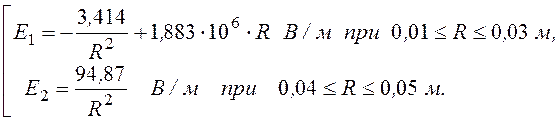
Ёмкость второго слоя диэлектрика на основании (12.9), задача 12.5:
С =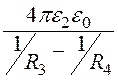
=
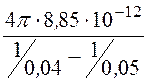= 22,24·10-12
Ф = 22,24 пФ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.