Электростатическое поле. Основные теоретические положения, страница 9

При  r ® 0  решение должно давать конечные значения j₂  и  E₂, что приводит к нулевому значению постоянной интегрирования   А₆= 0.           (*)

При  r ® ¥  решение должно привести наблюдателя в невозмущенное цилиндром поле, когда при  a= 0     E_1r= E₀ = U/d:                  А₂ = -E₀.         (*)

Поскольку потенциал определяется с точностью до постоянной, то примем                                                      А₁= 0.                                                  (*)

Тогда из шести уравнений (*), образующих систему, находим:

А₁= А₄ = 0;   А₆ = 0;    А₂ = -E₀;

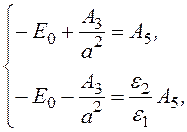Þ-2E₀ = А₅(1 +);   А₅ = -E₀;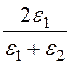

А₃ = а²(A₅ + E₀) = а²E₀(1 –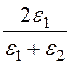) = а²E₀.

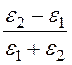Таким образом,

E_1r = E₀(1 +)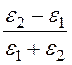cos a,     E_1a = -E₀(1 –)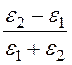sin a;

E_2r = E₀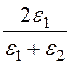cos a,                  E_2a = -E₀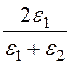sin a.

Модуль напряжённости поля в цилиндре

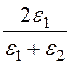E₂ == E₀= E₀·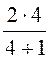= 1,6E₀, откуда следует, что поле внутри внесенного цилиндра равномерное.

Модуль напряжённости поля в первой среде на поверхности цилиндра при  r= a

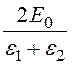
E₁ ==, где    E_1r(r = a) = E₀(1 +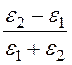)cos a = E₀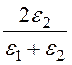cos a,

E_1a = -E₀(1 –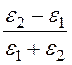)sin a = E₀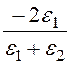sin a.

Наибольшие и наименьшие значения (экстремумы) напряжённости в изоляции определяются условием    [(e₂cos a)² +(e₁sin a)²] = 0.

e₂²·2cos a(-sin a) + e₁²·2sin a·cos a= 0;       sin2a·(e₁² – e₂²) = 0;   2a = kp ;

a = ½pk,   где  k = 0; ±1; ±2; …

При  k = 0   a = 0,      E_1min =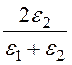E₀ = 0,4E₀;

k = 1   a = 90°,   E_1max =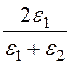E₀ = 1,6E₀.

Таким образом, требуется принять  E₀¢ = E_1проб/1,6 = 240/1,6 = 150 кВ/см, а чтобы не было ионизации воздуха –     E₀¢¢ = E_2проб/1,6 = 30/1,6 = 18,75 кВ/см.

Так как  E₀¢¢ < E₀¢, то при наличии воздушного цилиндра

U_max = E₀¢¢d = 18,75·2 = 37,5 кВ,

а рабочее напряжение   U_раб =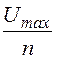== 12,5 кВ.

Задача 12.20. Диэлектрический шар радиу-сом  a = 2 см  находится в равномерном внешнем электрическом поле (рис. 12.23). Разность потенциалов между точками А и В  j_А – j_В = 5 В.  Сферические координаты точек: А(1 см, 60°, 90°); В(4 см, 30°, 90°). Средой, окружающей шар, является воздух   (ε₁ = 1).   Относительная диэлектрическая проницаемость диэлектрика шара  ε₂ = 3.  Определить модули вектора смещения в точках А и В.

Решение

Общее решение уравнения Лапласа в сферической системе координат получено методом разделения переменных [3]. Представим его здесь для случая, когда шар не заряжен.

Для первой области    R> a          j ₁ = A₁ + (A₂R +)cos q, тогда составляющие напряженности –   E_1R = -= -(A₂ –)cos q,

E_1q = -= (A₂ +)sin q.

Для второй области   R< a:

j₂ = A₄ + (A₅R +)cos q,        E_2R = -(A₅ –)cos q,        E_2q = (A₅ +)sin q.

Для определения постоянных интегрирования А₁÷А₆ воспользуемся граничными условиями. Из условия непрерывности потенциала на поверхности шара следует

А₁= А₄.                                               (*)

Условие   E_1t= E_2t   приводит к равенству  E_1q= E_2q  при   r= a:

А₂+= А₅ +.                                          (*)

условие  D_1n= D_2n  при  R= a  приводит к равенству e₁E_1R= e₂E_2R:

e₁(A₂ –) = e₂(A₅ –).                               (*)       

Условия в нуле  (R ® 0)  приводят к тому, что           А₆= 0,                 (*)

так как ни потенциал, ни напряжённость в центре сферы не могут быть бесконечными.   

Условия в бесконечности  (r ® ¥) позволяют определить А₂, поскольку там, где уже нет возмущения поля внесенной сферой,E_1r= E₀cos q = -A₂cos q.

Отсюда                                                         А₂= -E₀.                                  (*)

Поскольку потенциал определяется с точностью до постоянной, то примем                                                      А₁= 0.                                                  (*)

Тогда из шести уравнений (*), образующих систему, находим:

А₁= А₄ = 0;   А₆ = 0;    А₂ = -E₀;

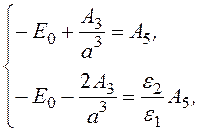Þ-3E₀ = А₅(2 +);   А₅ = -E₀;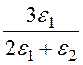

А₃ = а³(A₅ + E₀) = а³E₀(1 –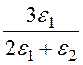) = а³E₀.

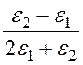Заданная условием задачи разность потенциалов:  j_А – j_В = 5 В.

На основании приведенного решения:

-E₀(-R_В +·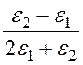)cos q_В + (-E₀)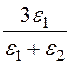R_Аcos q_А = 5.

Подставим расстояния в cм и получим:

-E₀(-4 +·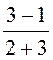) – E₀·1·= 5,  откуда        E₀= 1,672 В/cм  и