t1 = 80 мкКл/км, t2 = -12 мкКл/км,t3 = 0, a11 = a33 = 11,5·1010 м/ф,
a22 = 12,3·1010 м/ф, a12 = a23 = 0,2·1010 м/ф, a13 = 0,106·1010 м/ф.
После переключений t1¢ = t1, t2¢ = t2,j 3¢ = 0. Далее из первой группы формул Максвелла с теми же потенциальными коэффициентами определяем:
j 1¢ = 9950 В, j 2¢ = -88 В, t3¢ = -4,76 мкКл/км.
Дополнительно на тему подраздела 12.5 см. задачу 12.48, решенную с помощью ПЭВМ в системе MathCAD.
12.6. СИММЕТРИЧНЫЕ ПОЛЯ В СРЕДАХ С НЕОДНОРОДНЫМ ДИЭЛЕКТРИКОМ (e¹const)
В этих средах относительная диэлектрическая проницаемость eзависит от координат пространства, например, e= e(х). Так как
= e0
+
= ee0, то =– e0= e0(e– 1),
причём rсв = -div.
Часто диэлектрическая проницаемость задаётся с помощью зависимости d(е) или р(е), представленной графически или аналитически.
ЗАДАЧА 12.38. Диэлектрик плоского конденсатора неоднородный, e= e(х), зависимость для вектора поляризации Р = Рх = (а + bx2)Р0, где а = 1, b= 0,05 см-2, Р0 = 3,5·10-10 Кл/см2.
Определить плотность связанного заряда.
Решение
rсв = -div= -
= -2bxР0 = -2·0,05·x·3,5·10-10
= -0,35·10-10x Кл/см3, где x
[см].
ЗАДАЧА 12.39. Плоский конденсатор заполнен неоднородным диэлектриком с e(х) = 4d/(d+ x). Пластины конденсатора подключены к источнику постоянного напряжения U= 1 кВ.
Определить зависимости от координаты х напряжённости поля и значения вектора поляризации. Найти ёмкость и заряд конденсатора при заданном напряжении. Расстояние между пластинами d = 0,2 см, их площадь S= 4 см2.
Решение
Из граничного условия получаем D
= s=
= ee0E, откуда
E(х) =
=
=
.
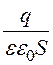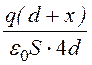Напряжение U =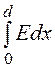
=
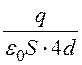(dx+
)
=
.
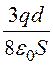Ёмкость конденсатора
С =
=
=
=
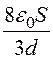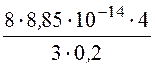4,75·10-12 Ф = 4,75 пФ.
Заряд и напряжённость поля
q =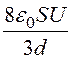
= СU = 4,75·10-12·1000
= 4,75·10-9 Кл,
Е(х) =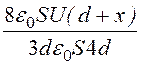
=
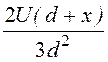= 16,7·(0,2 + х)
кВ/см, где x [см].
Вектор поляризации
Р(х) = e0E(e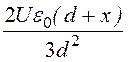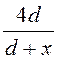– 1)=
(
– 1)=
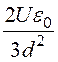(3d– х) =
= 14,75·10-10·(0,6 – х) Кл/см2.
Плотность связанного заряда
rсв = -div= -= 14,75·10-10
Кл/см3.
ЗАДАЧА 12.40. Между жилой коаксиального кабеля радиусом r1 = 1
см и оболочкой с внутренним радиусом r2 = 4 см находится диэлектрик с отно-сительной
диэлектрической проницаемостью e =
,где А = 16 см2,
r[см]. При
постоянном напряжении U = 1 кВ определить напряженность поля,
смещение, поляризацию и связанный объемный заряд, а также ёмкость на единицу
длины кабеля.
Решение
В соответствии с (12.5) D=
, тогда
напряженность поля
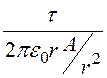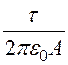Е(r) ==
=
r.
(*)
Напряжение U=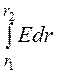
=
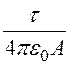(r22 – r12), откуда
t=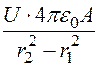
, (**)
емкость
С0 =
=
=
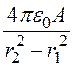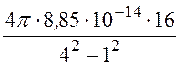= 1,19·10-12 Ф/см
= 0,119 нФ/м.
Подставляя (**) в (*), находим напряженность поля
Е(r) =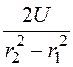
r
= 133,3r В/см,
где r[см].
Электрическое смещение
D = ee0E=
∙8,85∙10 -14·133,3r
=
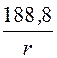·10 -12 Кл/см2.
Поляризация
P= e0E(e–
1) = 8,85∙10 -14∙133,3r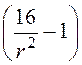
=
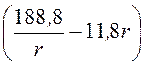·10
-12 Кл/см2.
Объёмная плотность связанного заряда
ρсв = -div=
-
[(188,8 – 11,8r2)·10 -12] = 23,6·10 -12
Кл/см3.
ЗАДАЧА 12.41. У цилиндрического конденсатора радиус жилы r1 = 1 см, внутренний радиус оболочки r2 = 5 см. Пространство между жилой и обо-лочкой заполнено сегнетоэлектриком, для которого зависимость модуля напряженности от модуля электрического смещения определяется выражением E= 1015(0,45D2+ 0,2·10 -6D), где Е [В/см], D [Кл/см2].
Конденсатор включен на постоянное напряжение U = 200 В.
Пренебрегая краевым эффектом и приняв потенциал жилы нулевым, найти зависимости Е(r) и j(r). Вычислить емкость единицы длины конденсатора.
Решение
По (12.5) D=, тогда
E(r)
= 1015(0,45D2+ 0,2·10 -6D) = 1015(0,45∙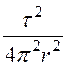
+
0,2∙10 -6∙). (*)
Приложенное напряжение
U=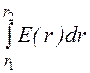
= 1015
,
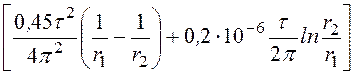2·10 -13 = t 2·9,12·10 -3 + t ·0,0512·10 -6.
Из этого уравнения t = 0,2653·10 -5 Кл/см.
Подставив в (*) значение t, находим
E(r) =
+
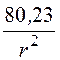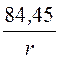В/см,
j(r) = -
=
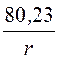– 84,45ln(r) + A.
Примем, что j= 0 при r = r1 = 1 см, тогда 0 = 80,23 – 84,45ln(r1) + A;
A
= 84,45ln(r1) – 80,23; j(r) =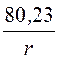+ 84,45ln – 80,23 В.
Емкость конденсатора С0 ==
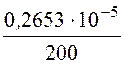= 1,327·10 -8
Ф/см.
12.7. Применение ПЭВМ для решения задач
Применять ПЭВМ целесообразно для решения задач, требующих большого объёма вычислительной работы. Ниже приведены решения некоторых подобных задач.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.