Электростатическое поле. Основные теоретические положения, страница 7

Пусть заряд внутренней жилы –  t.  Тогда напряжённости и потенциалы зон в соответствии с (12.5) и (12.8):   Е₁ =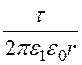;    j₁ = -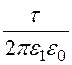ln(r) + А₁;

Е₂ =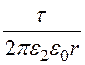;    j₂ = -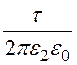ln(r) + А₂.

Максимальные напряжённости в областях:

Е_1max =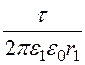;     Е_2max =.   

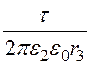Так как   e₁·r₁= 2 < e₂·r₃ = 4,  то    Е_2max < Е_1max = Е_max,    t = 2pe₁e₀r₁Е_max,

j₁ = -r₁Е_max·ln(r) + А₁;      j₂ = -r₁Е_max·ln(r) + А₂.

Пусть   j₁(r₂) = j₂(r₃) = 0,  тогда   А₁ = r₁Е_max·ln(r₂),   А₂ =r₁Е_max·ln(r₃),

j₁(r) = r₁Е_max·ln(r₂/r),    j₂(r) =r₁Е_max·ln(r₃/r).

Приложенное напряжение и ёмкость конденсатора

U = j₁(r₁) – j₂(r₄) = r₁Е_max·ln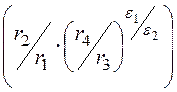= 46,37 кВ,

С ===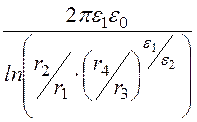 71,99 пФ.

12.3. ИСПОЛЬЗОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ СООТНОШЕ-НИЙ ПРИ РАСЧЁТЕ ПОЛЯ. Решение уравнений Пуассона и Лапласа.

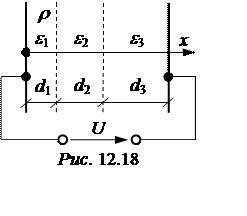Задача 12.16. Две проводящие пластины разделены тремя слоями диэлектрика с диэлектрическими проницаемостями   e₁ = 1,  e₂ = 2  и  e₃ = 3.   Толщина слоёв диэлектрика:   d₁ = 1 см,    d₂ = 2 см   и   d₃ = 3 см   (рис. 12.18).   Устройство подключено к источнику постоянного напряжения   U = 1000 В. Область первого диэлект-рика заполнена свободным зарядом с равномерной плотностью  r = 10^-10 Кл/см³.

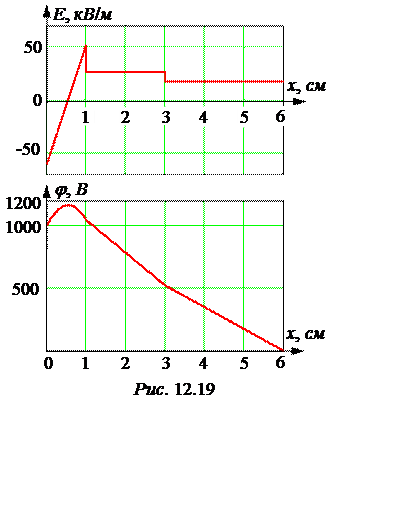
Построить графики изменения напряжён-ности электростатического поля и потенциала в зависимости от координат пространства, считая заземлённой правую пластину.

Решение

Задачу решим с помощью уравнений Пуассона и Лапласа:

Ñ ²j = -  или  0.

Скалярный лапласиан в декартовой системе координат (рис. 12.18) расписывается в соответствии с табл. 11.1 следующим образом:

Ñ ²j  =++.

Но в данной задаче потенциал зависит только от одной координаты х, то есть  == 0. Таким образом, для трёх различных областей получаем:           

Ñ ²j ==

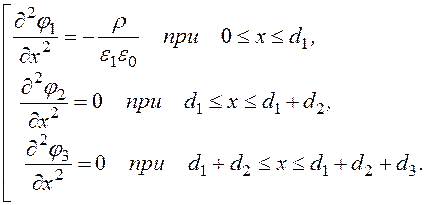
Двукратное интегрирование даёт:     j₁(х) = -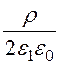х² + А₁х + А₂;

j₂(х) = А₃х + А₄;

j₃(х) = А₅х + А₆.

Этих выражений недостаточно для определения постоянных интегрирования А₁÷А₆, поэтому используем ещё формулы для напряженности поля из соотношения (12.1) с учётом табл. 11.1:

Е₁(х) = -=х – А₁;      Е₂(х) = -= -А₃;     Е₃(х) = -= -А₅.

Постоянные интегрирования находим, используя граничные условия.

Пусть при   х = d₁ + d₂ + d₃   j₃ = 0 (потенциал правой пластины), тогда

А₅·(d₁ + d₂ + d₃) + А₆ = 0.                          (*)

При   х = 0    j₁ = U  (потенциал левой пластины), тогда    А₂ = U.         (*)

При   х = d₁    j₁ = j₂,   то есть 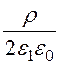   -d₁² + А₁d₁ + А₂ = А₃d₁ + А₄.         (*)

На границе двух диэлектриков равны нормальные составляющие векторов электростатической индукции –   D_1n = D_2n.   В данной задаче векторы  и  направлены по оси х, то есть имеют только нормальные составляющие. Поэтому при   х = d₁     e₁·Е₁ = e₂·Е₂;   то есть    d₁ – e₁·А₁ = -e₂·А₃.        (*)

При    х = d₁ + d₂      j₂ = j₃     и   e₂·Е₂ = e₃·Е₃, то есть

 А₃(d₁ + d₂) +А₄ = А₅(d₁ + d₂) + А₆;  (*)

-e₂·А₃ = -e₃·А₅.                         (*)

Шесть уравнений (*) образу-ют систему, решая которую, нахо-дим постоянные интегрирования.

Результат решения системы:

А₁ = 6,083·10⁴;      А₂ = 1000;

А₃ = -2,608·10⁴;     А₄ = 1304;     А₅ = -1,739·10⁴;    А₆ = 1043.    

Окончательно получаем

j(х) =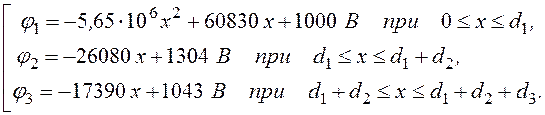

Е(х) =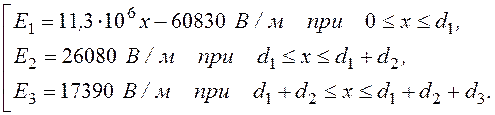 

Построенные по этим формулам графики приведены на рис. 12.19 1).

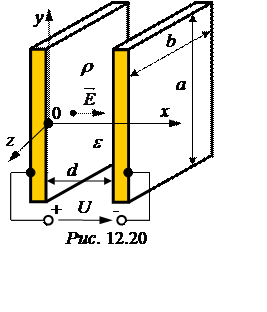
Задача 12.17. Между двумя плоскими электродами (рис. 12.20) напря-жённость поля изменяется по закону   E = E_x = E₀·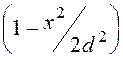,   E_y = 0,   E_z = 0. Расстояние между электродами  d= 5 мм  много меньше размеров пластин, причём  a= 25 см,  b= 1 м,  E₀ = 12 кB/см,  диэлектрическая проницаемость диэлектрика  e= 4.

Найти разность потенциалов между электродами, объёмную плотность свободного заряда и весь свободный заряд, заключённый между электродами.

Решение

Состояние поля определяется уравнением Пуассона    Ñ ²j = -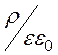.    Поскольку  d<< a  и d<<b, то можно пренебречь краевым эффектом. Тогда при расположении осей декартовой системы координат, как показано на рис. 12.20, jзависит только от х и   Ñ ²j =;

напряжённость поля

E(x) = -= E₀·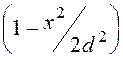, откуда    = -== -   и

r= -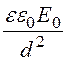·x = -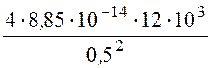·x = -1,7·10 ^-8·x Кл/см³,  где  x[см].

Напряжение между электродами

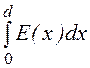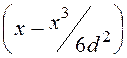
U== E₀·= E₀·(d– d/6) =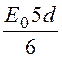==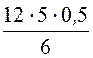 5 кB.