Силу, действующую на шар, можно определить через напряжённость, создаваемую в месте расположения шара тремя остальными зарядами. Но принцип наложения здесь нужно применять в векторной форме (рис. 12.31). Для удобства разложим векторы напряженностей на горизонтальную (х) и вертикальную (у) составляющие.
Е2у =
0, Е2х =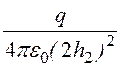 ,
,
 Е3x =
Е3x =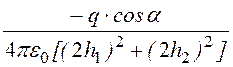 , Е3y =
, Е3y =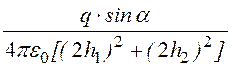 , где cosa =
, где cosa =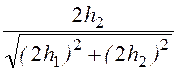 = 0,8944; sina = 0,4473.
= 0,8944; sina = 0,4473.
Е4х =
0, Е4у = -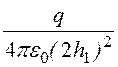 ,
,
Ех = Е2x + Е3x + Е4x = 0,40 В/м; Еу = Е2у + Е3у + Е4у = -5,12 В/м;
Е =![]() = 5,13 В/м;
F = q·E = 10-10·5,13 = 5,13·10-10 Н.
= 5,13 В/м;
F = q·E = 10-10·5,13 = 5,13·10-10 Н.
Примечание. Если бы вместо шара находился заряженный проводник (цилиндр), параллельный углу, то можно было бы ограничиться лишь первым зеркальным отображением, а затем воспользоваться группами формул Максвелла для двухпроводной линии.

Задача 12.29. Провода двухпроводной линии U = 500 В находятся в разных диэлектриках, как показано на рис. 12.32. Рассчитать заряд на проводе линии и её ёмкость. Геометрические размеры и свойства сред:
r0 = 0,2 см, r1 = 20 см, r2 = 40 см, e1 = 1, e2 = 2.
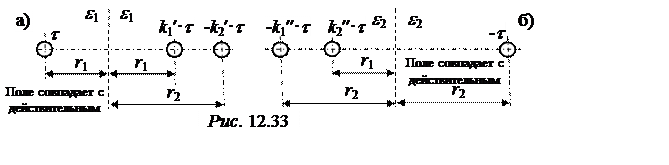 |
Пусть левый провод имеет заряд t, тогда правый – -t. Поскольку расчет поля нужно выполнить в обеих средах, расчет выполним, используя два рисунка (для каждой среды) – рис. 12.33,a и б. Коэффициенты неполного отражения:
k1¢ =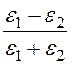 = -0,333; k2¢ =
= -0,333; k2¢ =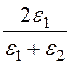 = 0,667;
= 0,667;
k1¢¢ =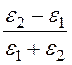 = 0,333; k2¢¢ =
= 0,333; k2¢¢ =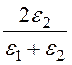 = 1,333.
= 1,333.
Потенциал точки О (рис. 12.32) будем считать равным нулю. Потенциал первого провода вычислим по рис. 12.33,a в соответствии с принципом наложения с учётом (12.10,а):
j 1 =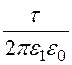 (ln
(ln![]() + k1¢·ln
+ k1¢·ln![]() – k2¢·ln
– k2¢·ln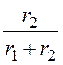 );
);
аналогично потенциал второго провода – по рис. 12.33,б:
j 2 =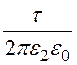 (-ln
(-ln![]() – k1¢¢·ln
– k1¢¢·ln![]() + k2¢¢·ln
+ k2¢¢·ln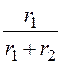 ).
).
Напряжение между проводами
U = j
1 – j 2 =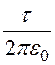 [e1-1·(ln
[e1-1·(ln![]() + k1¢·ln
+ k1¢·ln![]() – k2¢·ln
– k2¢·ln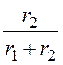 )
–
)
–
– e2-1·(-ln![]() – k1¢¢·ln
– k1¢¢·ln![]() + k2¢¢·ln
+ k2¢¢·ln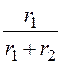 )] =
t ·15,06·1010.
)] =
t ·15,06·1010.
Отсюда t = U/15,06·1010 = 0,332·10-8 Кл/м.
Ёмкость линии С0 = t/U = 6,64 пФ/м.
 12.5. ГРУППЫ ФОРМУЛ
МАКСВЕЛЛА. ЧАСТИЧНЫЕ ЁМКОСТИ.
12.5. ГРУППЫ ФОРМУЛ
МАКСВЕЛЛА. ЧАСТИЧНЫЕ ЁМКОСТИ.
ЗАДАЧА 12.30. Линия передачи (рис. 12.34) состоит из трёх проводов радиуса r0 = = 0,6 см. Высота подвеса проводов h1 = h3 = 6 м, h2 = 5,2 м. Расстояния между проводами по горизонтали d12 = 2 м, d23 = 1,6 м. Напряжения между проводами U12 = 60 кВ, U23 = 40 кВ. Определить потенциал и заряд каждого из проводов.
Решение
Определяем расстояния между проводами, а также между проводами и их зеркальными изображениями (рис. 12.34):
а12 =![]() =
=![]() = 2,13 м,
= 2,13 м,
а13 =![]() =
=![]() = 3,6 м,
= 3,6 м,
а23 =![]() =
=![]() =1,79 м,
=1,79 м,
b12 =![]() =
=![]() = 11,4 м,
= 11,4 м,
b13 =![]() =
=![]() = 12,5 м,
= 12,5 м,
b23 =![]() =
=![]() = 11,3 м.
= 11,3 м.
Вычисляем потенциальные коэффициенты (на единицу длины):
a11
= a33 =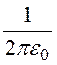 ln
ln![]() =
=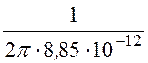 ln
ln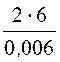 = 13,66·1010 м/ф,
= 13,66·1010 м/ф,
a22
=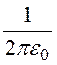 ln
ln![]() =
=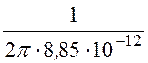 ln
ln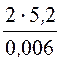 = 13,41·1010 м/ф,
= 13,41·1010 м/ф,
a12
= a21 =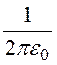 ln
ln![]() =
=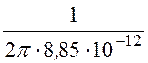 ln
ln![]() = 3,02·1010 м/ф,
= 3,02·1010 м/ф,
a13
= a31 =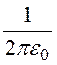 ln
ln![]() =
=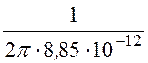 ln
ln![]() = 2,24·1010 м/ф,
= 2,24·1010 м/ф,
a23
= a32 =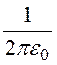 ln
ln![]() =
=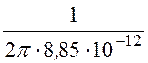 ln
ln![]() = 3,32·1010 м/ф.
= 3,32·1010 м/ф.
![]() Для
определения зарядов проводов используем первую группу формул Максвелла: j 1 = t1a11 + t2a12 + t3a13,
Для
определения зарядов проводов используем первую группу формул Максвелла: j 1 = t1a11 + t2a12 + t3a13,
j 2 = t1a21 + t2a22 + t3a23,
j 3 = t1a31 + t2a32 + t3a33.
Недостающие для определения шести неизвестных величин уравнения записываем, используя дополнительные условия задачи:
j 1 – j 2 = U12, j 2 – j 3 = U23, и так как провода образуют изолированную, не связанную с землёй систему, то t1 + t2 + t3 = 0.
Решая полученную систему из шести уравнений, находим искомое:
t1 = 0,466·10 -6 Кл/м, t2 = -0,058·10 -6 Кл/м,t3 = -0,408·10 -6 Кл/м,
j 1 = 52,8 кВ, j 2 = -7,2 кВ,j 3 = -47,2 кВ.
ЗАДАЧА 12.31. Решить задачу 12.26, используя группы формул Максвелла.
Ответы. a11 =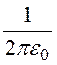
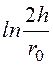 = 9,522·1010 м/Ф;
j1 = U= 1000 B;
= 9,522·1010 м/Ф;
j1 = U= 1000 B;
t1 = j1/a11 = 1,05·10 -8 Кл/м; С0 = С11 = 10,5 пФ/м.
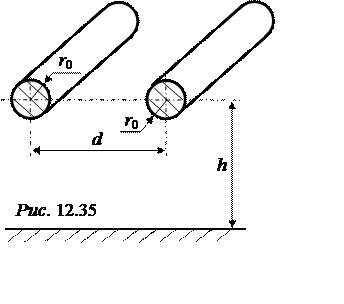
ЗАДАЧА 12.32. Определить частич-ные и рабочую (C0) ёмкости одного метра двухпроводной воздушной линии электро-передачи (рис. 12.35), если h= d= 2 м, r0 = 1 см.
Ответы. a12 = d= 2 м,
b12 =![]() = 2
= 2![]() м;
м;
a11 = a22 = 10,77·1010 м/Ф,
a12 = a21 = 1,45·1010 м/Ф;
b11 = b22 = 9,46·10 -12 Ф/м,
 b12 = b21 = -1,27·10 -12 Ф/м;
b12 = b21 = -1,27·10 -12 Ф/м;
C11 = C22 = 8,19 пФ/м, C12 = C21 = 1,27 пФ/м;
C0 = 5,37 пФ/м.
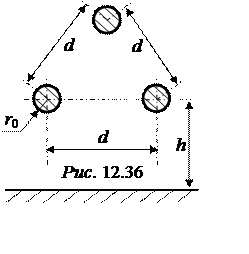
ЗАДАЧА 12.33. Определить частичные ёмкос-ти трёхпроводной воздушной линии электропере-дачи (рис. 12.36), если r0 = 1 см, h= 6 м, d= 2 м.
Ответы. a12 = a13 = a23 = d = 2 м,
b12 = b23
=![]() = 13,77 м,
= 13,77 м,
b13 =![]() = 12,17 м,
= 12,17 м,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.