ЗАДАЧА 12.42. Решить задачу 12.17 с помощью ПЭВМ. Распечатку программы см. в приложении к разделу 12.
ЗАДАЧА 12.43. Решить задачу 12.23 с помощью ПЭВМ. Распечатку программы см. в приложении к разделу 12.
ЗАДАЧА 12.44. Решить задачу 12.24 с помощью ПЭВМ. Распечатку программы см. в приложении к разделу 12.
 ЗАДАЧА 12.45.
В изоляции коаксиального кабеля (рис. 12.43) имеется равномерно распределённый
заряд с объёмной плотностью r= 10 -10 Кл/м3. Внутренний
и на-ружный радиусы диэлектрического слоя – r1 = 1 см и r2 = = 10 см, длина l= 100 м, относительная диэлектрическая
проницаемость – e= 4. определить
запасённую в электри-ческом поле энергию.
ЗАДАЧА 12.45.
В изоляции коаксиального кабеля (рис. 12.43) имеется равномерно распределённый
заряд с объёмной плотностью r= 10 -10 Кл/м3. Внутренний
и на-ружный радиусы диэлектрического слоя – r1 = 1 см и r2 = = 10 см, длина l= 100 м, относительная диэлектрическая
проницаемость – e= 4. определить
запасённую в электри-ческом поле энергию.
Решение
Задачу решаем, интегрируя уравнение Лапласа для области r1 < r< r2. Аналогично задаче 12.18 записываем:
j(r) = -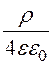 r2 + А1ln(r) + А2; Е(r) =
r2 + А1ln(r) + А2; Е(r) =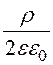 r –
r –![]() .
.
Граничные условия: j(r=r2) = 0, Е(r=r1) = 0. Решая полученную систему уравнений, находим постоянные интегрирования А1 и А2.
Запасённую в электрическом поле энергию можно найти двумя способами.
В первом способе воспользуемся формулой для энергии заряда dq слоя толщиной dr, расположенного на расстоянии r от оси:
dW = 0,5dq·j = 0,5r ·2prl·dr·j;
W =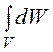 =
=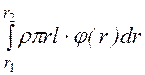 =
0,533 Дж.
=
0,533 Дж.
Во втором способе используем формулу для объёмной плотности энергии электростатического поля: w = 0,5ee0Е2.
wdV = 0,5ee0Е2·2prl·dr = ee0Е2·prl·dr,
W
=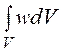 =
=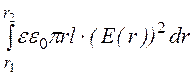 =
0,533 Дж.
=
0,533 Дж.
MathCAD-программа и ответы приведены в Приложении к разделу 12.
Примечание. Ответы для потенциала и энергии в буквенном виде следующие:
j(r) =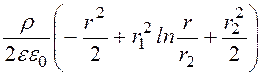 ; W =
; W =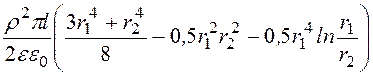 .
.
ЗАДАЧА 12.46. Решить задачу 12.12 с помощью ПЭВМ. Распечатку программы см. в приложении к разделу 12.

Задача 12.47. Между проводами двухпроводной линии электропередачи (рис. 12.44) действует напряжение U = 220 кВ. Построить график зависимости от координаты х напряжённости поля на оси, соединяющей провода. Определить максимальную напряжённость поля, если d = 2 м, r0 = 1 см. Смещением электрических и геометрических осей пренебречь.
Решение
Напряжённость электростатического поля, создаваемого левым и правым проводами линии отдельно на оси х, в соответствии с (12.5):
E¢ =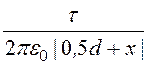 ,
E¢¢ =
,
E¢¢ =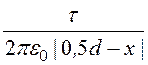 .
.
Формулы для потенциала любой точки в пространстве между проводами в соответствии с (12.10):
j ¢ =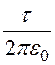 ln
ln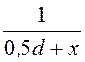 , j
¢¢ =
, j
¢¢ =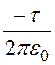 ln
ln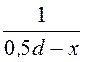 , j
= j ¢ + j ¢¢ =
, j
= j ¢ + j ¢¢ =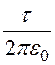 ln
ln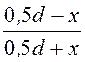 .
.
Тогда напряжение между проводами
U = j(х=-0,5d+r0) – j(х=0,5d-r0) =
=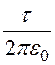 ln
ln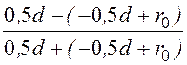 –
–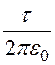 ln
ln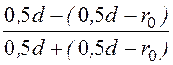 =
=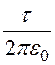 ln
ln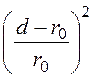 =
=
=![]() ln
ln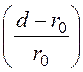 .
.
Отсюда заряд провода линии t=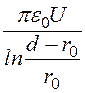 .
.
Формула емкости двухпроводной линии на единицу длины
С0 =![]() =
=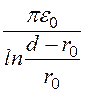 .
.
В пространстве между проводами, как видно из рис. 12.44, напряжённости от действия отдельных проводов складываются, а снаружи – вычитаются, внутри проводов поле отсутствует:
при -0,5d +r0 < x< 0,5d – r0E = E¢ + E¢¢, при |x| > 0,5d + r0E = E¢ – E¢¢.
Как видно из графика, приведенного в MathCAD-программе, максимальное значение напряжённости наблюдается в точке с координатой x= 0,5d – r0 (на поверхности провода): Emax = E(х=0,5d-r0) = 21 кВ/см.
MathCAD-программа и ответы приведены в Приложении к разделу 12.
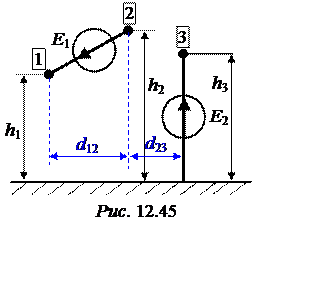
Задача 12.48. В системе провод-ников, расположенных в воздухе вблизи проводящей поверхности, действуют два источника ЭДС, как показано на рис. 12.45: Е1 = 5 кВ, Е2 = 2 кВ. Радиусы всех проводов одинаковы и равны r0 = 10 мм. Высота под-веса проводников h1 = 5 м, h2 = 7 м, h3 = 6 м. Расстояния между проводниками по горизонтали d12 = 3 м, d23 = 2 м.
Определить потенциал и заряд на единицу длины каждого проводника. Дополнительно вычислить частичные ёмкости системы проводников.
Решение задачи осуществляется по алгоритму и по формулам задачи 12.30. MathCAD-программа и ответы приведены в Приложении к разделу 12.
C. 61-67 – см. файл «Приложение к разделу 12».
1) Для записи ответа в одну строку при построения графиков в системе MathCAD можно использовать функцию Хэвисайда (функцию включения, единичную ступенчатую функцию), которая в системе MathCAD обозначается F. Например, для данной задачи:
j(х) = j1·[F(x) – F(x–d1)] + j2·[F(x–d1) – F(x–d1–d2)] + j3·[F(x–d1–d2) – F(x–d1–d2–d3)].
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.