линейная
плотность заряда t =![]() =
=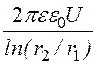 ;
;
напряжённость и потенциал (формулы (12.5) и (12.10,а)):
Е(r) =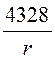 В/м, j(r) = 4328ln
В/м, j(r) = 4328ln![]() В, где r[м];
В, где r[м];
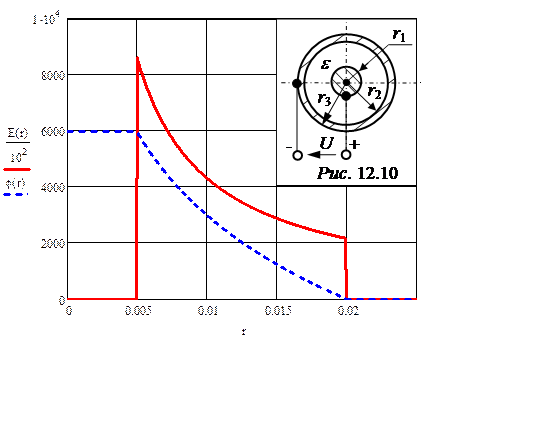
графики Е(r) и j(r) на рис. 12.10.
 Объёмная плотность энергии в диэлектрике wЭ =
Объёмная плотность энергии в диэлектрике wЭ =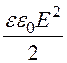 =
=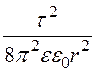 .
.
Энергия поля, запасённая в кабеле
wЭ =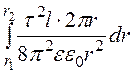 =
=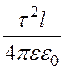 ln
ln![]() =
=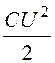 = 57,73·10 -9
Дж.
= 57,73·10 -9
Дж.
ЗАДАЧА 12.10. Рассчитать поле цилиндрического луча электронов – r = -10-10 Кл/см3, e = 2, d = 2 мм. Задачу решить с помощью теоремы Гаусса в интегральной форме.
Решение
Теорема
Гаусса в интегральной форме – 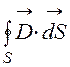 = Sq. В цилиндриче-ской системе
координат
= Sq. В цилиндриче-ской системе
координат
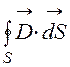 = D·2prl
(см. (12.4)); E =
= D·2prl
(см. (12.4)); E =![]() = -
= -![]() , j(r) = -
, j(r) = -![]() (см. задачу 12.8).
(см. задачу 12.8).
В области r < d/2
Sq = r ·pr2l;
D1 = ½rr, E1(r) =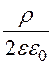 ·r;
j 1(r) = -
·r;
j 1(r) = -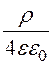 ·r2 + A1.
·r2 + A1.
Пусть j1 = 0 при r = 0. Тогда А1 = 0. После подстановки числовых значений имеем: Е1(r) = -2,825·106·r В/м; j 1(r) = 1,412·106·r2 В.
В области r > d/2 Sq = r ·p(d/2)2l;
D2 =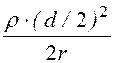 ; E2(r) =
; E2(r) =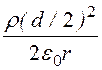 ; j 2(r) = -
; j 2(r) = -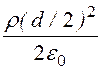 ·ln(r) + A2.
·ln(r) + A2.
при r = ½d j2(d/2) = j1(d/2) = 1,412·106·(10-3)2 = 1,41 В, отсюда
А2 = j 2(d/2) +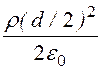 ln(d/2) = 1,41 – 5,65·ln(0,001) =
40,44.
ln(d/2) = 1,41 – 5,65·ln(0,001) =
40,44.
Таким образом, E2(r) = -![]() В/м; j 2(r) = 5,65·ln(r) + 40,44 В.
В/м; j 2(r) = 5,65·ln(r) + 40,44 В.
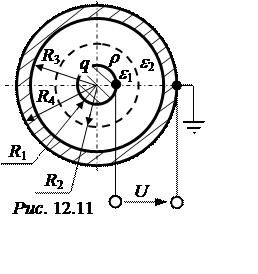
Задача 12.11. Внутри заземлённого полого металлического шара с внутренним и наружным радиусами R3 = 3,2 см и R4 = 3,6 см, соответственно, (рис. 12.11) расположен ещё один металлический шар радиуса R1 = 0,8 см, причём последний несёт на себе заряд q = 2,5·10-8 Кл. В устройстве имеется область, заряженная равно-мерно с объёмной плотностью r = -10-10 Кл/см3, обладающая относительной диэлектрической про-ницаемостью e1 = 2, и область, не содержащая сво-бодных зарядов с относительной диэлектрической проницаемостью e2 = 1,5. Размер R2 = 1,6 см.
Рассчитать и построить графики зависимости напряжённости электростатического поля и потенциала от расстояния до центра шара.
Решение
В областях 0 < R < R1, R3 < R < R4 находится проводящий материал, поэтому электростатическое поле в этих областях отсутствует – E = 0, D = 0, j = const. Поле отсутствует также за пределами шара, поскольку оболочка шара заземлена.
В областях R1 < R < R2 и R2 < R <
R3 расчёт
поля выполним с помощью теоремы Гаусса в интегральной форме: 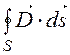 = Sq. На основании (12.2)
= Sq. На основании (12.2)
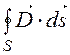 = D·4pR2.
= D·4pR2.
В области R1 < R<
R2 Sq = q
+ r ·![]() p(R3 – R13). Тогда
p(R3 – R13). Тогда
D1 =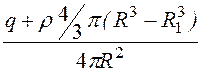 ; Е1 =
; Е1 =![]() =
=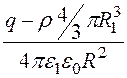 +
+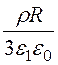 .
.
На основании (12.8), j 1 = -![]() =
=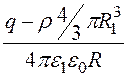 –
–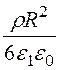 + А1.
+ А1.
В области R2 < R <
R3 Sq
= q
+ r ·![]() p(R23 – R13). Тогда
p(R23 – R13). Тогда
D2 =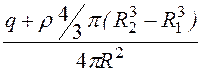 ; Е2 =
; Е2 =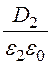 =
=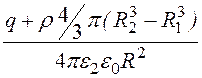 ;
;
j 2 = -![]() =
=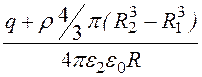 + А2.
+ А2.
Постоянные интегрирования А1 и А2 определим, зная, что j 2(R3) = 0, и учтя, что потенциал – функция непрерывная.
j 2(R3) =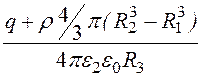 + А2
= 0, отсюда
+ А2
= 0, отсюда
А2 = -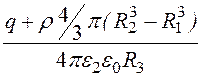 = -4402.
= -4402.
Таким образом, после подстановки числовых значений получим:
j 2(R) =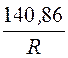 – 4402 В, Е2(R) =
– 4402 В, Е2(R) =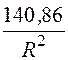 В/м, где
R [м].
В/м, где
R [м].
при r = R2 j 1(R2) = j 2(R2) =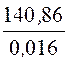 – 4402 = 4402 В.
– 4402 = 4402 В.
То есть 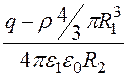 –
–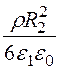 + А1 = 4402 и А1
= -2804.
+ А1 = 4402 и А1
= -2804.
Таким образом, после подстановки числовых значений получим:
j 1(R) =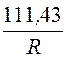 + 9,42·105·R2 – 2804 В, Е1(R) =
+ 9,42·105·R2 – 2804 В, Е1(R) =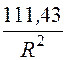 –18,83·105·R
В/м.
–18,83·105·R
В/м.
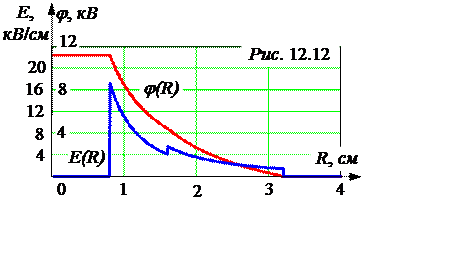
Графики j(R) и Е(R) представлены на рис. 12.12.
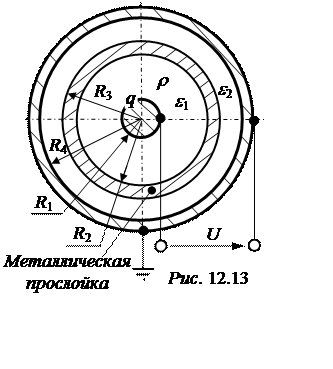
Задача 12.12. Два проводящих шара (рис. 12.13) разделены двумя слоями диэлектрика с относительными диэлектри-ческими проницаемостями e1 = 2 и e2 = 1 с металлической прослойкой между ними. Радиусы зон: R1 = 1 см, R2 = 3 см, R3 = 4 см и R4 = 5 см. Шары подключены к источ-нику постоянного напряжения U = 1000 В. Область первого диэлектрика заполнена свободным зарядом с равномерной объёмной плотностью r = 10-10 Кл/см3.
Построить графики изменения напряженности электростатического поля и потенциала в зависимости от координат пространства, считая наружную оболочку заземлённой. Рассчитать также ёмкость слоя, в котором r = 0.
Задачу решить с помощью теоремы Гаусса в интегральной форме.
Решение
Допустим, что внутренний шар несёт на себе заряд q. Далее поле в диэлектрических областях (R1 < R < R2 и R3 < R < R4) можно рассчитать аналогично тому, как это сделано в задаче 12.11.
В области R1 < R < R2
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.