a11 = a33 = 12,76·1010 м/Ф, a22 = 13,21·1010 м/Ф,
a12 = a23 = 3,47·1010 м/Ф, a13 = 3,25·1010 м/Ф,
b11 = b33 = 8,783·10 -12 Ф/м, b22 = 8,54·10 -12 Ф/м,
b12 = b23 = -1,852·10 -12 Ф/м, b13 = -1,732·10 -12 Ф/м, C11 = C33 = 5,2 пФ/м,
C22 = 4,836 пФ/м, C12 = C23 = 1,852 пФ/м, C13 = 1,732 пФ/м.
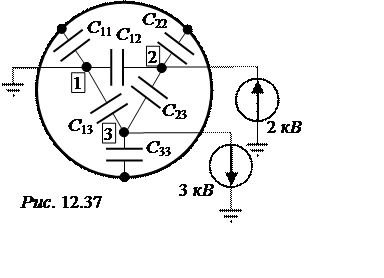ЗАДАЧА 12.34. Собственные и частичные ёмкости трёхжильного
кабеля, соответственно, равны: C11 = C22 = C33 = 0,064 мкФ/км,
C12 = C23 = = C13 = 0,076 мкФ/км.
При испытании кабеля в лаборатории одна из жил ка-беля была заземлена, вторая
имела по-тенциал j 2 = 2 кВ, третья – j 3 = -3 кВ. Оболочка кабеля
не заземлена.
Найти потенциал оболочки и заряды жил.
Решение
В
соответствии с условием задачи составим схему рис. 12.37, для которой на
основании III группы формул Максвелла t1 = j 1¢C11 + U12C12 + U13C13,
t2 = U21C21 + j 2¢C22 + U23C23,
t3 = U31C31 + U32C32 + j 3¢C33, где потенциалы жил определяются по отношению к оболочке.
Если оболочку рассматривать в виде четвёртого проводника, то можно составить уравнение и для неё с учётом того, что она не соединена с землей а, значит, не несёт заряда: t4 = (j 4 – j 1)C11 + (j 4 – j 2)C22 + (j 4 – j 3)C33 = 0.
Здесь потенциалы определяются по отношению к земле.
Так как C11 = C22 = C33 и j 1 = 0, j 2 = 2 кВ,j 3 = -3 кВ, то
j 4 =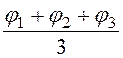
=
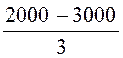= -333
В.
Возвращаемся к системе уравнений и, зная, что
j 1¢ = j 1 – j 4 = 333 В, U21 = -U12 = 2000 В, U13 = -U31 = 3000 В,
U23 = -U32 = 5000 В, j 2¢ = j 2 – j 4 = 2333 В, j 3¢ = j 3 – j 4 = -2667 В, получаем t1 = (333·0,064 – 2000·0,076 + 3000·0,076)·10 -6 = 97·10 -6 Кл/км,
t2 = (2000·0,076 + 2333·0,064 + 5000·0,076)·10 -6 = 681·10 -6 Кл/км,
t3 = (-3000·0,076 – 5000·0,076 – 2667·0,064)·10 -6 = -779·10 -6 Кл/км.
Задача 12.35. Рассчитать частичную и рабочую емкости двухпроводной экранированной линии (рис. 12.38), если:
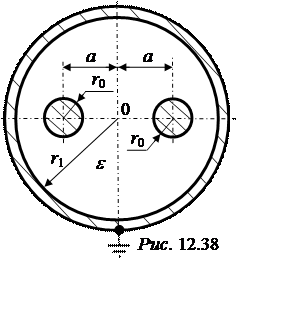r0 = 2 мм, а = 4 см, r1 = 10 см, e = 4.
При расчете принять, что оболочка (экран) заземлена.
Решение
Примем, что под действием источника напряжения U, подключенного к проводам, произошло разделение зарядов между первым (левым) проводом и вторым (правым). Тогда первый провод несет заряд t1 = t на единицу длины линии, а второй – t2 = -t.
Для дальнейшего расчета воспользуемся методом зеркальных изображений для оси, расположенной внутри цилиндра. Расчетная схема для поля внутри цилиндра имеет вид рис. 12.39, причём а∙b = r12.
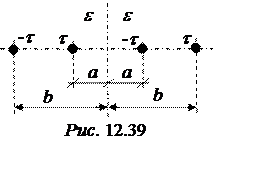В нашем примере b =
=
= 25 см.
Первая группа формул Максвелла для системы заряженных тел, расположенных вблизи цилиндрической проводящей поверхности:
j 1 = t1a11 + t2a12 ,
j 2 = t1a21 + t2a22 , где
a11 = a22 =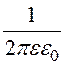
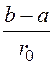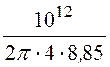ln
=
ln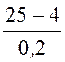
=
2,091·1010 м/ф,
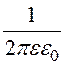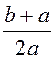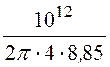a12 = a21 =ln
=ln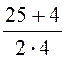
=
0,579·1010 м/ф.
Вторая
группа формул Максвелла: t1 = b11j 1 + b12j 2,
t2 = b21j 1 + b22j 2, где
b11 = b22 =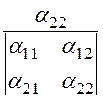
=
=
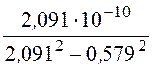0,518·10 -10 ф/м,
b12 = b21 =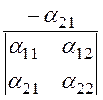
=
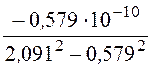= -0,143·10
-10 ф/м.
Третья
группа формул Максвелла: t1 = U10C11 + U12C12,
t2 = U21C21 + U20C22, где C11 = C22 = b11 + b12 = 0,375·10 -10 ф/м, C12 = C21 = -b12 = 0,143·10 -10 ф/м.
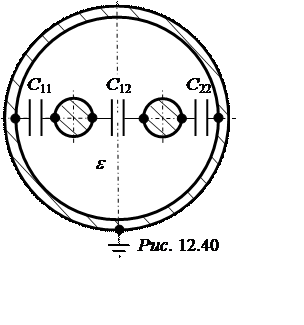Частичные емкости линии показаны на рис. 12.40.
Рабочая емкость двухпроводной экранированной линии на единицу длины:
С0 = С12
+
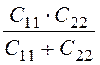= (0,143 + 
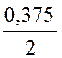)∙10
-10 =
= 0,331∙10 -10 Ф/м.
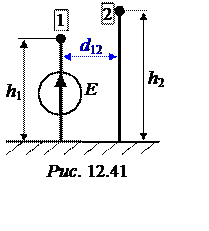ЗАДАЧА 12.36.
В системе из двух проводников (рис. 12.41), расположенных в воздухе вблизи
проводящей поверхности, действует источник ЭДС Е = 127 В,
причём второй проводник соединён с землёй. Геометрические размеры: r0 = 6 мм, d12 = 1 м, h1 = 3 м, h2 = 4 м.
Определить заряды проводов.
Ответы. а12 =
м, b12 = 5 м,
a11 = 12,4·1010 м/ф, a22 = 12,9·1010 м/ф,
a12 = 2,9·1010 м/ф, j 1 = 127 В, j 2 = 0,
t1 = 0,852·10 -11 Кл/м, t2 = -0,191·10 -11 Кл/м.
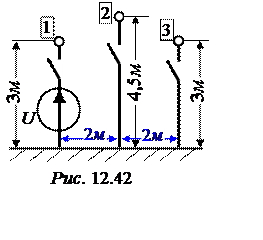ЗАДАЧА 12.37.
Определить потенциалы и заряды системы проводов, изображённой на рис. 12.42,
где рубильники 1 и 2 замкнуты, а 3 – разомкнут, U = 10 кВ,
радиус проводов r0 = 5 мм.
Как изменится решение, если сначала провод 2 отключается от земли, затем провод 1 отключается от источника и, наконец, провод 3 соединяется с землёй.
Ответы. До переключений j 1 = 10 кВ, j 2 = 0,j 3 = 0,605 кВ,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.